题目内容
6．若方程$\frac{1}{4-{x}^{2}}$+2=$\frac{k}{x-2}$有增根，求k的值．分析 增根是分式方程化为整式方程后产生的使分式方程的分母为0的根．把增根代入化为整式方程的方程即可求出k的值．
解答 解：方程两边都乘（x+2）（x-2），得
-1+2（x2-4）=k（x+2）
∵原方程增根为x=2，x=-2．
∴把x=2代入整式方程，得k=-$\frac{1}{4}$．
x=-2时，-1+2（x2-4）=k（x+2）不成立．
点评 本题考查了分式方程的增根，增根确定后可按如下步骤进行：化分式方程为整式方程；把增根代入整式方程即可求得相关字母的值．
练习册系列答案
相关题目
17．
2016无锡“五一”车展期间，某公司对参观车展的且有购车意向的消费者进行了随机问卷调查，共发放900份调查问卷，并收回有效问卷750份．工作人员对有效调查问卷作了统计，其中，将消费者年收入的情况整理后，制成表格如下：
将消费者打算购买小车的情况整理后，绘制出频数分布直方图（如图，尚未绘完整）．（注：每组包含最小值不包含最大值．）
请你根据以上信息，回答下列问题：
（1）根据表格中信息可知，被调查消费者的年收入的平均数是6.48万元．（精确到0.01）
（2）请在右图中补全这个频数分布直方图．
（3）打算购买价格10万元以下（不含10万元）小车的消费者人数占被调查消费者人数的百分比是50%．
（4）本次调查的结果，是否能够代表全市所有居民的年收入情况和购车意向？为什么？
2016无锡“五一”车展期间，某公司对参观车展的且有购车意向的消费者进行了随机问卷调查，共发放900份调查问卷，并收回有效问卷750份．工作人员对有效调查问卷作了统计，其中，将消费者年收入的情况整理后，制成表格如下：| 年收入（万元） | 4.8 | 6 | 7.2 | 9 | 10 |
| 被调查的消费者人数（人） | 150 | 338 | 160 | 60 | 42 |
请你根据以上信息，回答下列问题：
（1）根据表格中信息可知，被调查消费者的年收入的平均数是6.48万元．（精确到0.01）
（2）请在右图中补全这个频数分布直方图．
（3）打算购买价格10万元以下（不含10万元）小车的消费者人数占被调查消费者人数的百分比是50%．
（4）本次调查的结果，是否能够代表全市所有居民的年收入情况和购车意向？为什么？
小张骑车往返于甲、乙两地，距甲地的路程y（千米）与时间x（时）的函数图象如图所示．
11．已知|x|=3，|y|=2，且xy＜0，则x-y的值等于（ ）
| A． | 5 | B． | 5或-5 | C． | -5 | D． | -5或1 |
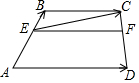如图，在梯形ABCD中，AD∥BC，AD=3，BC=2，点E、F分别在两腰上，
如图，在平面直角坐标系中．直线y=-x+3与x轴交于点B，与y轴交于点C，抛物线y=ax2+bx+c经过B，C两点，与x轴负半轴交于点A，连结AC，tan∠CAB=3