题目内容
4.计算:(1)3$\sqrt{18}$-$\frac{1}{2}$$\sqrt{32}$+7$\sqrt{\frac{1}{8}}$
(2)2$\sqrt{12}$÷$\frac{1}{2}$$\sqrt{50}$×$\frac{1}{2}$$\sqrt{\frac{3}{4}}$
(3)($\sqrt{3}$-1)2+$\frac{2}{2-\sqrt{3}}$.
分析 (1)先把各二次根式化为最简二次根式,然后合并同类二次根式;
(2)先把各二次根式化为最简二次根式,然后进行二次根式的乘除运算;
(3)先利用完全平方公式计算,再进行分母有理化,然后合并即可.
解答 解:(1)原式=9$\sqrt{2}$-2$\sqrt{2}$+$\frac{7\sqrt{2}}{4}$
=$\frac{35\sqrt{2}}{4}$;
(2)原式=4$\sqrt{3}$÷$\frac{5\sqrt{2}}{2}$×$\frac{\sqrt{3}}{4}$
=4×$\frac{2}{5}$×$\frac{1}{4}$×$\sqrt{3×\frac{1}{2}×3}$
=$\frac{3\sqrt{2}}{5}$;
(3)原式=3-2$\sqrt{3}$+1+2(2+$\sqrt{3}$)
=4-2$\sqrt{3}$+4+2$\sqrt{3}$
=8.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.四边形ABCD中,对角线AC与BD相交于点O,给出下列四组条件:(1)AB∥CD,AD=BC.(2)AB∥DC,AD∥BC.(3)AB=DC,AD=BC.(4)OA=OC,OB=OD.其中一定能判定这个四边形是平行四边形的条件有( )
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
19. 在平行四边形ABCD中,若∠A=30°,AB边上的高为8,则BC的长为( )
在平行四边形ABCD中,若∠A=30°,AB边上的高为8,则BC的长为( )
 在平行四边形ABCD中,若∠A=30°,AB边上的高为8,则BC的长为( )
在平行四边形ABCD中,若∠A=30°,AB边上的高为8,则BC的长为( )| A. | 16 | B. | 8 | C. | 8$\sqrt{2}$ | D. | 8$\sqrt{3}$ |
9.若a<b,则下列各式中不成立的是( )
| A. | a+2<b+2 | B. | -3a<-3b | C. | 2-a>2-b | D. | 3a<3b |
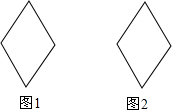 如图1、2是两个全等的菱形,边长为2cm,最小内角为60°.
如图1、2是两个全等的菱形,边长为2cm,最小内角为60°.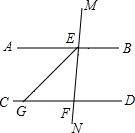 如图,AB∥CD,直线MN分别交AB、CD于点E、F,EG平分∠AEN交CD于点G.若∠MEB=80°,求∠EGD的度数.
如图,AB∥CD,直线MN分别交AB、CD于点E、F,EG平分∠AEN交CD于点G.若∠MEB=80°,求∠EGD的度数.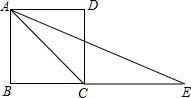 如图,点E是正方形ABCD边BC延长线上的一点,且CE=AC,求∠E的度数.
如图,点E是正方形ABCD边BC延长线上的一点,且CE=AC,求∠E的度数.