题目内容
14.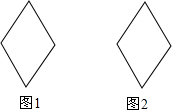 如图1、2是两个全等的菱形,边长为2cm,最小内角为60°.
如图1、2是两个全等的菱形,边长为2cm,最小内角为60°.(1)分别对图1、图2个各设计一个不同的分割方案,并将分割后的若干块拼成一个与原菱形等面积的矩形,要求:先在已知图1、2中画出分割线(虚线),再画出拼成的矩形并注明长、宽的长度;
(2)分别求出第(1)问中矩形的长边与对角线所成的夹角的正弦值.
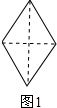
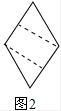
分析 (1)分割线如图1沿着菱形的对角线分割即可,图2沿着菱形的两条高分割即可;拼成的矩形如图3、图4所示;
(2)设矩形的长边与对角线所成的夹角为α,根据勾股定理求出矩形的对角线=$\sqrt{{2}^{2}+(\sqrt{3})^{2}}$=$\sqrt{7}$,即可得到结果.
解答 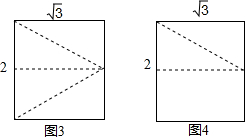
 解:(1)分割线如图1、图2所示
解:(1)分割线如图1、图2所示
拼成的矩形如图3、图4所示;
(2)设矩形的长边与对角线所成的夹角为α,
∵矩形的对角线=$\sqrt{{2}^{2}+(\sqrt{3})^{2}}$=$\sqrt{7}$,
∴sinα=$\frac{\sqrt{3}}{\sqrt{7}}$=$\frac{\sqrt{21}}{7}$.
∴矩形的长边与对角线所成的夹角的正弦值为$\frac{\sqrt{21}}{7}$.
点评 本题考查了作图-应用与设计作图,勾股定理菱形的性质,矩形的性质,正确领会题意是解题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
13.某商场用18万元购进A、B两种商品,其进价和售价如下表:
(1)若销售完后共获利3万元,该商场购进A、B两种商品各多少件;
(2)若购进B种商品的件数不少于A种商品的件数的6倍,且每种商品都必须购进.
①问共有几种进货方案?
②要保证利润最高,你选择哪种进货方案?
| A | B | |
| 进价(元/件) | 1200 | 1000 |
| 售价(元/件) | 1380 | 1200 |
(2)若购进B种商品的件数不少于A种商品的件数的6倍,且每种商品都必须购进.
①问共有几种进货方案?
②要保证利润最高,你选择哪种进货方案?
19.在某样本方差的计算公式s2=$\frac{1}{10}$[(x1-8)2+(x2-8)2+…+(x10-8)2]中,数字10和8依次表示样本的( )
| A. | 容量,方差 | B. | 平均数,容量 | C. | 容量,平均数 | D. | 方差、平均数 |
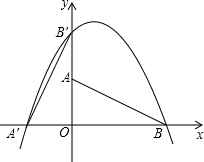 如图,直角坐标系中Rt△ABO,其顶点为A(0,1)、B(2,0)、O(0,0),将此三角板绕原点O逆时针旋转90°,得到Rt△A′B′O.
如图,直角坐标系中Rt△ABO,其顶点为A(0,1)、B(2,0)、O(0,0),将此三角板绕原点O逆时针旋转90°,得到Rt△A′B′O.