在平行四边形ABCD中.若∠A=30°.AB边上的高为8.则BC的长为( )A．16B．8C．8$\sqrt{2}$D．8$\sqrt{3}$ 题目和参考答案——青夏教育精英家教网—

题目内容

19．

在平行四边形ABCD中，若∠A=30°，AB边上的高为8，则BC的长为（　　）

A．

B．

C．

8$\sqrt{2}$

D．

8$\sqrt{3}$

分析由直角三角形的性质得到AD的长，再根据平行四边形的性质即可得到结论．

解答解：如图，过D作DE⊥AB于E，
则DE=8，∠AED=90°，
∵∠A=30°，
∴AD=2DE=16，
∵四边形ABCD是平行四边形，
∴BC=AD=16，
故选A．

点评本题考查了平行四边形的性质，直角三角形的性质，正确的画出图形是解题的关键．

练习册系列答案

10．《一千零一夜》中有这样一段文字：有一群鸽子，其中一部分在树上欢歌，另一部分在地上觅食，树上一只鸽子对地上觅食的鸽子说：“若从你们中飞来一只，则树下的鸽子就是整个鸽群的$\frac{1}{3}$；若从树上飞下去一只，则树上，树下的鸽子数一样多．”你知道树上树下共有12只．

7．如果mn＜0，且m＜0，则点P（m²，n-m）在（　　）

14．（1）请在横线上填写合适的内容，完成下面的证明：
如图1，AB∥CD，求证：∠B+∠D=∠BED．
证明：过点E引一条直线EF∥AB
∴∠B=∠BEF，（两直线平行，内错角相等）
∵AB∥CD，EF∥AB
∴EF∥CD（如果两条直线都与第三条直线平行，那么这两条直线也互相平行）
∴∠D=∠FED（两直线平行，内错角相等）
∴∠B+∠D=∠BEF+∠FED
即∠B+∠D=∠BED．
（2）如图2，AB∥CD，请写出∠B+∠BED+∠D=360°的推理过程．
（3）如图3，AB∥CD，请直接写出结果∠B+∠BEF+∠EFD+∠D=540°．

4．计算：
（1）3$\sqrt{18}$-$\frac{1}{2}$$\sqrt{32}$+7$\sqrt{\frac{1}{8}}$
（2）2$\sqrt{12}$÷$\frac{1}{2}$$\sqrt{50}$×$\frac{1}{2}$$\sqrt{\frac{3}{4}}$
（3）（$\sqrt{3}$-1）²+$\frac{2}{2-\sqrt{3}}$．

11．

如图，已知四边形ABCD，对角线AC和BD相交于O，下面选项不能得出四边形ABCD是平行四边形的是（　　）

	A．	同位角都相等
	B．	同一平面内，不相交的两条直线叫做平行线
	C．	过一点有且只有一条直线与已知直线平行
	D．	两直线平行，同旁内角相等

9．

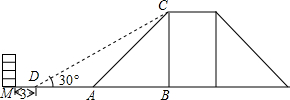如图是某市一座人行过街天桥，天桥高CB=5米，斜坡AC的坡度为1：1，为了方便行人推车过天桥，市政部门决定降低坡度，使新坡面的傾斜角为30°．若新坡脚前需留3m的人行道，问离原坡脚A处7m的建筑物M是否需要拆除，请说明理由．（$\sqrt{3}$≈1.73）

试题分类