题目内容
有一列数a1、a2、a3…an,从第二个数开始,每一个数都等于与它前面那个数的倒数的差,若a1=2,则a2010为 .
考点:规律型:数字的变化类,倒数
专题:
分析:分别求出n=2、3、4…时的情况,观察它是否具有周期性,再把2010代入求解即可.
解答:解:a1=2,a2=1-
=
,a3=1-2=-1,a4=1+1=2;
数列以2、
、-1依次不断循环出现;
2010÷3=670;
所以a2010=a3=-1.
故答案为:-1.
| 1 |
| 2 |
| 1 |
| 2 |
数列以2、
| 1 |
| 2 |
2010÷3=670;
所以a2010=a3=-1.
故答案为:-1.
点评:此题考查数字的变化规律.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.而具有周期性的题目,找出周期是解题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 如图,在长为100米,宽为80米的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化.设修建的道路宽为x米,如果绿化面积为7644米2,那么可列方程为( )
如图,在长为100米,宽为80米的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化.设修建的道路宽为x米,如果绿化面积为7644米2,那么可列方程为( )| A、8000-100x-80x=7644 |
| B、(100-x) (80-x)+x2=7644 |
| C、(100-x) (80-x)=7644 |
| D、100x+80x=356 |
近年来,全国各地房价不断上涨,我市2011年12月份的房价平均每平方米为12400元,比2009年同期的房价平均每平方米上涨了5800元.假设这两年我市房价的平均增长率为x,则由题意可列出关于x的方程为( )
| A、(1+x)2=12400 |
| B、5800(1+x)2=12400 |
| C、(12400-5800)(1+x)=12400 |
| D、(12400-5800)(1+x)2=12400 |
 如图,等边三角形ABC的边BC上的高为6,AD是BC边上的中线,M是AD上的动点,E是AC的中点.求EM+CM的最小值.
如图,等边三角形ABC的边BC上的高为6,AD是BC边上的中线,M是AD上的动点,E是AC的中点.求EM+CM的最小值.
 如图,正方形EFGH的外接圆⊙O是正方形ABCD的内切圆,试求AB:EF的值.
如图,正方形EFGH的外接圆⊙O是正方形ABCD的内切圆,试求AB:EF的值.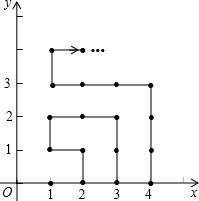 如图,在平面直角坐标系中,有若干个横、纵坐标分别为整数的点,其顺序按图中点的坐标分别为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…的规律排列,根据这个规律,第2015个点的横坐标为
如图,在平面直角坐标系中,有若干个横、纵坐标分别为整数的点,其顺序按图中点的坐标分别为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…的规律排列,根据这个规律,第2015个点的横坐标为