题目内容
如图，正方形EFGH的外接圆⊙O是正方形ABCD的内切圆，试求AB：EF的值．考点：正多边形和圆
专题：
分析：设大正方形的边长为1，那么圆的直径为1，根据“正方形的面积=边长×边长”求出大正方形的面积，从而得出△HGF的面积：1×（1÷2）÷2=0.25，即可得出正方形EFGH的面积：0.25×2=0.5，再根据相似得出边之比．
解答：
解：如图，大正方形的边长为1，则HF=1，
则S正方形ABCD=1，
S正方形EFGH=2S△HGF=2×1×（1÷2）÷2=0.5，
∵正方形ABCD∽正方形EFGH，
∴AB：EF=
=
．
解：如图，大正方形的边长为1，则HF=1，则S正方形ABCD=1，
S正方形EFGH=2S△HGF=2×1×（1÷2）÷2=0.5，
∵正方形ABCD∽正方形EFGH，
∴AB：EF=
| 2：1 |
| 2 |
点评：本题考查了正多边形和圆，灵活运用三角形面积和正方形面积公式是解题的关键．
练习册系列答案
相关题目
若用A、B、C、分别表示有理数a、b、c，0为原点，如图所示．已知a＜c＜0，b＞0．
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，令x0=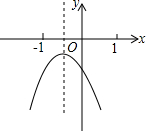
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，在下列五个结论中：
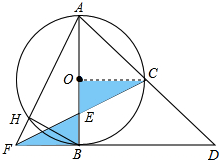如图，以AB为直径的⊙O切△AFD的边FD于点B，AD交⊙O于点C，且C是弧AB的中点，CF交AB于点E，且E为OB中点．若AF交⊙O于点H，连接BH，若OA=4，求BH的长．