题目内容
如图，等边三角形ABC的边BC上的高为6，AD是BC边上的中线，M是AD上的动点，E是AC的中点．求EM+CM的最小值．考点：轴对称-最短路线问题,等边三角形的性质
专题：
分析：连接BE，交AD于M，则BE就是PE+PC的最小值，根据等边三角形的三线合一的性质从而证得BE=AD=6．
解答：
解：如图所示：
∵AD是BC边上的中线，
∴AD等边三角形ABC的边BC上的高，
∴AD是BC的垂直平分线，
连接BE，交AD于M，则BE就是EM+CM的最小值，
∵E是AC的中点，
∴BE是等边三角形ABC的边AC上的高，
∴BE=AD，
∵等边三角形ABC的边BC上的高为6，
∴BE=AD=6．
∴EM+CM的最小值是6．
解：如图所示：∵AD是BC边上的中线，
∴AD等边三角形ABC的边BC上的高，
∴AD是BC的垂直平分线，
连接BE，交AD于M，则BE就是EM+CM的最小值，
∵E是AC的中点，
∴BE是等边三角形ABC的边AC上的高，
∴BE=AD，
∵等边三角形ABC的边BC上的高为6，
∴BE=AD=6．
∴EM+CM的最小值是6．
点评：本题考查了等边三角形的性质和轴对称等知识的综合应用，解题关键是对这些知识的熟练掌握及灵活运用．
练习册系列答案
相关题目
如图，已知S△ABC=S△ABD，求证：AB∥CD．
如图所示矩形纸片ABCD，长AD=9cm，宽AB=3cm，将纸片折叠，使点D与点B重合，则DE=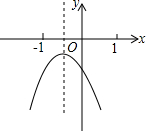
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，在下列五个结论中：