题目内容
20. 在2016年巴西里约奥运会上,中国女排克服重重困难,凭借顽强的毅力和超强的实力先后战胜了实力同样超强的巴西队,荷兰队和塞尔维亚队,获得了奥运冠军,为祖国和人民争了光.
在2016年巴西里约奥运会上,中国女排克服重重困难,凭借顽强的毅力和超强的实力先后战胜了实力同样超强的巴西队,荷兰队和塞尔维亚队,获得了奥运冠军,为祖国和人民争了光.如图,已知女排球场的长度OD为18米,位于球场中线处的球网AB的高度为2.24米,一队员站在点O处发球,排球从点O的正上方2米的C点向正前方飞去,排球的飞行路线是抛物线的一部分,当排球运行至离点O的水平距离OE为6米时,到达最高点F,以O为原点建立如图所示的平面直角坐标系.
(1)当排球运行的最大高度为2.8米时,求排球飞行的高度y(单位:米)与水平距离x(单位:米)之间的函数关系式.
(2)在(1)的条件下,这次所发的球能够过网吗?如果能够过网,是否会出界?请说明理由.
(3)喜欢打排球的李明同学经研究后发现,发球要想过网,球运行的最大高度h(米)应满足h>2.32,但是他不知道如何确定h的取值范围,使排球不会出界(排球压线属于没出界),请你帮忙解决并指出使球既能过网又不会出界的h的取值范围.
分析 (1)利用抛物线的顶点F的坐标为(6,2.8),将点(0,2)代入解析式求出即可;
(2)利用当x=9时,y=-$\frac{1}{45}$(x-6)2+2.8=2.6,当y=0时,-$\frac{1}{45}$(x-6)2+2.8=-0.4,分别得出即可;
(3)设抛物线解析式为y=a(x-6)2+h,由点C(0,2)得解析式为y=$\frac{2-h}{36}$(x-6)2+h,再依据x=18时y≤0即可得h的范围.
解答 解:(1)由题意可得抛物线的顶点F的坐标为(6,2.8),
设抛物线的解析式为y=a(x-6)2+2.8,
将点C(0,2)代入,得:36a+2.8=2,
解得:a=-$\frac{1}{45}$,
∴y=-$\frac{1}{45}$(x-6)2+2.8;
(2)当x=9时,y=-$\frac{1}{45}$(9-6)2+2.8=2.6>2.24,
当x=18时,y=-$\frac{1}{45}$(18-6)2+2.8=-0.4<0,
∴这次发球可以过网且不出边界;
(3)设抛物线解析式为y=a(x-6)2+h,
将点C(0,2)代入,得:36a+h=2,即a=$\frac{2-h}{36}$,
∴此时抛物线解析式为y=$\frac{2-h}{36}$(x-6)2+h,
根据题意,得:$\frac{144(2-h)}{36}$+h≤0,
解得:h≥$\frac{8}{3}$,
又∵h>2.32,
∴h≥$\frac{8}{3}$
答:球既能过网又不会出界的h的取值范围是h≥$\frac{8}{3}$.
点评 此题主要考查了二次函数的应用题,求范围的问题,可以利用临界点法求出自变量的值,再根据题意确定范围.

练习册系列答案
相关题目
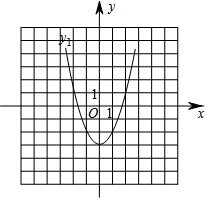 如图为抛物线y1=x2-3,且抛物线y2是由抛物线y1向右平移2个单位得到的.
如图为抛物线y1=x2-3,且抛物线y2是由抛物线y1向右平移2个单位得到的. 如图,⊙O为锐角三角形ABC的外接圆,若∠BAO=18°,则∠C的度数为72°.
如图,⊙O为锐角三角形ABC的外接圆,若∠BAO=18°,则∠C的度数为72°. 如图,△ABC的三个顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1).
如图,△ABC的三个顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1).