题目内容
15. 如图,△ABC的三个顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1).
如图,△ABC的三个顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1).(1)在图中画出将△ABC先向右平移3个单位,再向上平移2个单位后得到的△A1B1C1;
(2)在图中画出△ABC绕原点O顺时针旋转90°后得到的△A2B2C2;
(3)在(2)的条件下,计算点A所经过的路径的长度.
分析 (1)利用点平移的坐标规律写出点A1、B1、C1的坐标,然后描点即可;
(2)利用网格特点和旋转的性质画出点A、B、C的对应点A2、B2、C2,从而得到△A2B2C2;
(3)先计算出OA,然后利用弧长公式计算.
解答 解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;
(3)OA=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
所以点A所经过的路径的长度=$\frac{90•π•2\sqrt{5}}{180}$=$\sqrt{5}$π.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了平移变换.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
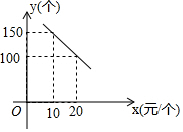 某旅游风景区出售一种纪念品,该纪念品的成本为12元/个,这种纪念品的销售价格为x(元/个)与每天的销售数量y(个)之间的函数关系如图所示.
某旅游风景区出售一种纪念品,该纪念品的成本为12元/个,这种纪念品的销售价格为x(元/个)与每天的销售数量y(个)之间的函数关系如图所示. 如图,一次函数的图象经过(2,0)和(0,-4),根据图象求$\sqrt{{k}^{2}-2kb+{b}^{2}}$的值.
如图,一次函数的图象经过(2,0)和(0,-4),根据图象求$\sqrt{{k}^{2}-2kb+{b}^{2}}$的值. 在2016年巴西里约奥运会上,中国女排克服重重困难,凭借顽强的毅力和超强的实力先后战胜了实力同样超强的巴西队,荷兰队和塞尔维亚队,获得了奥运冠军,为祖国和人民争了光.
在2016年巴西里约奥运会上,中国女排克服重重困难,凭借顽强的毅力和超强的实力先后战胜了实力同样超强的巴西队,荷兰队和塞尔维亚队,获得了奥运冠军,为祖国和人民争了光. 某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成20份),并规定:顾客每购物满200元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得50元、30元、20元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转盘,那么可直接获得10元的购物券.
某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成20份),并规定:顾客每购物满200元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得50元、30元、20元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转盘,那么可直接获得10元的购物券.