题目内容
10．
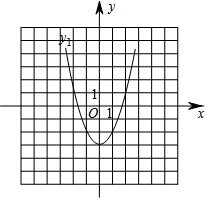如图为抛物线y1=x2-3，且抛物线y2是由抛物线y1向右平移2个单位得到的．（1）写出抛物线y2的函数表达式，并在直角坐标系中画出抛物线y2．
（2）过点（0，a-3）（a为实数）作x轴的平行线，与抛物线y1，y2共有4个不同的交点，设这4个交点的横坐标分别是x1，x2，x3，x4．
①求a的取值范围；
②若x1＜x2＜x3＜x4，试求x4-x3+x2-x1的最大值．
分析 （1）根据抛物线平移的规律即可得到结论；
（2）根据函数解析式图象可知，若过点（0，a-3）（a为实数）作x轴的平行线，与函数y1、y2的图象共有4个不同的交点时，则a-3＞-3且a≠1，再分别求出y1、y2分别等于a-3时x的值，分0＜a＜1和a＞1时x1、x2、x3、x4的值，从而代入x4-x3+x2-x1可知最值情况，
解答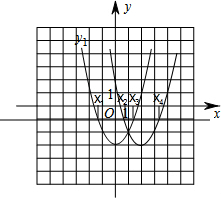 
解：（1）∵抛物线y2是由抛物线y1向右平移2个单位得到的，
∴y2═（x-2）2-3，
如图1所示；
（2）①∵y1=x2-3，y2=（x-2）2-3，
结合图象，由题意，知：a-3＞-2，
∴a＞1，
∴a的取值范围为：a＞0且a≠1；
②令y1=a-3，则x2-3=a-3 解得x=±$\sqrt{a}$，
令y2=a-3，则（x-2）2-3=a-3，解得x=2±$\sqrt{a}$，
因为x1＜x2＜x3＜x4，显然x1=-$\sqrt{a}$，x4=2+$\sqrt{a}$，
∵a≠1，则a的取值范围是a＞0且a≠1，
当0＜a＜1时，$\sqrt{a}$＜2-$\sqrt{a}$，∴x2=$\sqrt{a}$，x3=2-$\sqrt{a}$，
∴x4-x3+x2-x1=4$\sqrt{a}$＜4，
当a＞1时，$\sqrt{a}$＞2-$\sqrt{a}$，
∴x3=$\sqrt{a}$，x2=2-$\sqrt{a}$，
∴x4-x3+x2-x1=4，
综上所述，x4-x3+x2-x1的最大值为4．
点评 本题考查函数的综合问题，涉及待定系数法求解析式，二次函数图象的性质，一元二次方程的解法和数形结合的思想，综合程度较高，需要学生利用数形结合的思想解决问题．
练习册系列答案
相关题目
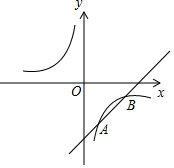如图，已知一次函数y=kx+b与反比例函数y=$\frac{m}{x}$交于A（1，-3），B（a，-1）两点．
在2016年巴西里约奥运会上，中国女排克服重重困难，凭借顽强的毅力和超强的实力先后战胜了实力同样超强的巴西队，荷兰队和塞尔维亚队，获得了奥运冠军，为祖国和人民争了光．