题目内容
9.(1)如图1,在平行四边形ABCD中,已知点E在AB上,点F在CD上,且AE=CF.求证:DE=BF;(2)如图2,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,求∠CDA的度数.

分析 (1)根据平行四边形的性质可证AB∥CD,AB=CD,又由已知可证BE=DF,即证四边形BEDF是平行四边形,故DE=BF;
(2)连接OD,构造直角三角形,利用OA=OD,可求得∠ODA=35°,从而根据∠CDA=∠CDO+∠ODA计算求解.
解答 (1)证明:∵四边形ABCD是?ABCD,
∴AB∥CD,AB=CD,
∵AE=CF,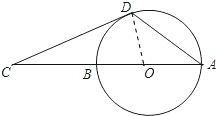
∴BE=DF,
∴四边形BEDF是平行四边形,
∴DE=BF;
(2)解:连接OD,则∠ODC=90°,∠COD=70°;
∵OA=OD,
∴∠ODA=∠A=$\frac{1}{2}$∠COD=35°,
∴∠CDA=∠CDO+∠ODA=90°+35°=125°.
点评 本题考查了平行四边形的判定和性质,切线的性质,三角形的外角与内角的关系,等边对等角求解.

练习册系列答案
相关题目
14.下列式子正确的是( )
| A. | a2+a3=a5 | B. | (a2)3=a5 | C. | a+2b=2ab | D. | (-ab)2=a2b2 |
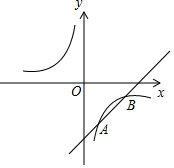 如图,已知一次函数y=kx+b与反比例函数y=$\frac{m}{x}$交于A(1,-3),B(a,-1)两点.
如图,已知一次函数y=kx+b与反比例函数y=$\frac{m}{x}$交于A(1,-3),B(a,-1)两点. 在2016年巴西里约奥运会上,中国女排克服重重困难,凭借顽强的毅力和超强的实力先后战胜了实力同样超强的巴西队,荷兰队和塞尔维亚队,获得了奥运冠军,为祖国和人民争了光.
在2016年巴西里约奥运会上,中国女排克服重重困难,凭借顽强的毅力和超强的实力先后战胜了实力同样超强的巴西队,荷兰队和塞尔维亚队,获得了奥运冠军,为祖国和人民争了光. 某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成20份),并规定:顾客每购物满200元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得50元、30元、20元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转盘,那么可直接获得10元的购物券.
某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成20份),并规定:顾客每购物满200元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得50元、30元、20元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转盘,那么可直接获得10元的购物券.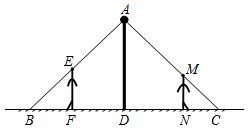 如图,小强和小华共同站在路灯下,小强的身高EF=1.8m,小华的身高MN=1.5m,他们的影子恰巧等于自己的身高,即BF=1.8m,CN=1.5m,且两人相距4.7m,则路灯AD的高度是4m.
如图,小强和小华共同站在路灯下,小强的身高EF=1.8m,小华的身高MN=1.5m,他们的影子恰巧等于自己的身高,即BF=1.8m,CN=1.5m,且两人相距4.7m,则路灯AD的高度是4m.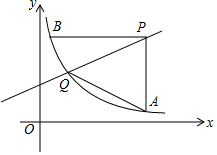 如图,直线y=$\frac{1}{2}$x+m与反比例函数y=$\frac{k}{x}$(x>0)的图象交于Q点,点B(1,6)在反比例函数的图象上,过B作BP∥x轴交直线y=$\frac{1}{2}$x+m于点P,过点P作PA∥y轴交双曲线于点A,连结AQ,BQ.
如图,直线y=$\frac{1}{2}$x+m与反比例函数y=$\frac{k}{x}$(x>0)的图象交于Q点,点B(1,6)在反比例函数的图象上,过B作BP∥x轴交直线y=$\frac{1}{2}$x+m于点P,过点P作PA∥y轴交双曲线于点A,连结AQ,BQ.