题目内容
5.如图,长为120km的某段线路AB上有甲、乙两车,分别从南站A和北站B同时出发相向而行,到达B,A后立刻返回到出发站停止,速度均为40km/h,设甲车,乙车据南站A的路程分别为y甲,y乙(km)行驶时间为t(h).(1)图2已画出y甲与t的函数图象,其中a=120,b=3,c=6.
(2)分别写出0≤t≤3及3<t≤6时,y乙与时间t之间的函数关系式.
(3)在图2中补画y乙与t之间的函数图象,并观察图象得出在整个行驶过程中两车相遇的次数.
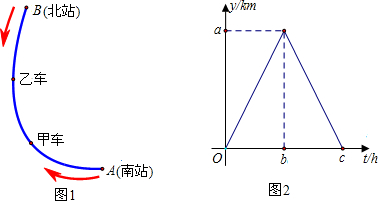
分析 (1)根据题意和函数图象可以得到a、b、c的值;
(2)根据题意和(1)中的答案可以分别求得当0≤t≤3及3<t≤6时,y乙与时间t之间的函数关系式;
(3)根据题意可以画出相应的函数图象,根据函数图象可以得到在整个行驶过程中两车相遇的次数.
解答 解:(1)由题意可和函数图象可得,
a=120,b=120÷40=3,c=2×3=6,
故答案为:120,3,6;
(2)当0≤t≤3时,设y乙与时间t之间的函数关系式为:y乙=kt+b,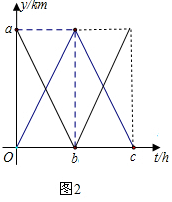
$\left\{\begin{array}{l}{b=120}\\{3k+b=0}\end{array}\right.$,得$\left\{\begin{array}{l}{k=-40}\\{b=120}\end{array}\right.$,
即当0≤t≤3时,y乙与时间t之间的函数关系式为:y乙=-40t+120;
当3<t≤6时,设y乙与时间t之间的函数关系式为:y乙=mt+n,
$\left\{\begin{array}{l}{3m+n=0}\\{6m+n=120}\end{array}\right.$,得$\left\{\begin{array}{l}{m=40}\\{n=-120}\end{array}\right.$,
即当3<t≤6时,y乙与时间t之间的函数关系式为:y乙=40t-120;
(3)y乙与t之间的函数图象如右图2所示,
由图象可知,整个行驶过程中两车相遇次数为2.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

练习册系列答案
相关题目
16.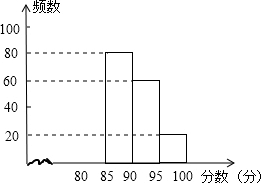 某校组织了一次G20知识竞赛活动,根据获奖同学在竞赛中的成绩制成的统计图表如下,仔细阅读图表解答问题:
某校组织了一次G20知识竞赛活动,根据获奖同学在竞赛中的成绩制成的统计图表如下,仔细阅读图表解答问题:
(1)求出表中a,b,c的数值,并补全频数分布直方图;
(2)获奖成绩的中位数落在哪个分数段?
(3)估算全体获奖同学成绩的平均分.
 某校组织了一次G20知识竞赛活动,根据获奖同学在竞赛中的成绩制成的统计图表如下,仔细阅读图表解答问题:
某校组织了一次G20知识竞赛活动,根据获奖同学在竞赛中的成绩制成的统计图表如下,仔细阅读图表解答问题:| 分数段 | 频数 | 频率 |
| 80≤x<85 | a | 0.2 |
| 85≤x<90 | 80 | b |
| 90≤x<95 | 60 | c |
| 95≤x<100 | 20 | 0.1 |
(2)获奖成绩的中位数落在哪个分数段?
(3)估算全体获奖同学成绩的平均分.
14.下列式子正确的是( )
| A. | a2+a3=a5 | B. | (a2)3=a5 | C. | a+2b=2ab | D. | (-ab)2=a2b2 |

 在2016年巴西里约奥运会上,中国女排克服重重困难,凭借顽强的毅力和超强的实力先后战胜了实力同样超强的巴西队,荷兰队和塞尔维亚队,获得了奥运冠军,为祖国和人民争了光.
在2016年巴西里约奥运会上,中国女排克服重重困难,凭借顽强的毅力和超强的实力先后战胜了实力同样超强的巴西队,荷兰队和塞尔维亚队,获得了奥运冠军,为祖国和人民争了光.
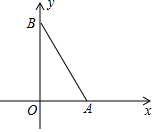 在平面直角坐标系中,O为原点,A点坐标为($\sqrt{3}$,0),B点坐标为(0,4),求△AOB的面积.
在平面直角坐标系中,O为原点,A点坐标为($\sqrt{3}$,0),B点坐标为(0,4),求△AOB的面积.