题目内容
14. 如图,已知△ABC中,AB=10cm,AC=8cm,BC=6cm,如果点P由点B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
如图,已知△ABC中,AB=10cm,AC=8cm,BC=6cm,如果点P由点B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:(1)当t为何值时,PQ∥BC?
(2)是否存在某时刻t,使线段PQ恰好把△ABC的面积平分?若存在,求出此时t的值;若不存在,请说明理由.
分析 (1)证△APQ∽△ABC,推出$\frac{AP}{AB}=\frac{AQ}{AC}$,代入得出$\frac{10-2t}{10}=\frac{2t}{8}$,求出方程的解即可;
(2)假设存在某时刻t,使线段PQ恰好把△ABC的面积平分,得出方程$-\frac{5}{6}{t}^{2}+6t=\frac{1}{2}×\frac{1}{2}$×8×6,求出此方程无解,即可得出答案.
解答 解:(1)由题意知:BP=2t,AP=10-2t,AQ=2t,
∵PQ∥BC,
∴△APQ∽△ABC,
∴$\frac{AP}{AB}=\frac{AQ}{AC}$,
即$\frac{10-2t}{10}=\frac{2t}{8}$,
解得:t=$\frac{20}{9}$,
∴当t=$\frac{20}{9}$时,PQ∥BC.
(2)假设存在某时刻t,使线段PQ恰好把△ABC的面积平分,
则${S}_{△APQ}=\frac{1}{2}{S}_{△ABC}$,
即$-\frac{5}{6}{t}^{2}+6t=\frac{1}{2}×\frac{1}{2}$×8×6,
t2-5t+10=0,
∵△=52-4×1×10=-15<0,
∴此方程无解,
即不存在某时刻t,使线段PQ恰好把△ABC的面积平分.
点评 本题考查了三角形的面积,勾股定理的逆定理,相似三角形的性质和判定的应用,主要考查学生综合运用进行推理和计算的能力.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
9.已知三角形两边的长分别是6和9,则这个三角形第三边的长可能为( )
| A. | 2 | B. | 3 | C. | 7 | D. | 16 |
3.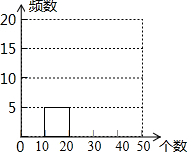 体育课的一个项目是排球30秒对墙垫球,为了解某校七年级学生此项目平时的训练情况,随机抽取了该校部分七年级学生进行测试,根据测试结果,制作了如下尚不完整的频数分布表,其中第1组垫球个数在10≤x<20的人数占被调查人数的10%.
体育课的一个项目是排球30秒对墙垫球,为了解某校七年级学生此项目平时的训练情况,随机抽取了该校部分七年级学生进行测试,根据测试结果,制作了如下尚不完整的频数分布表,其中第1组垫球个数在10≤x<20的人数占被调查人数的10%.
(1)表中a=9;
(2)补全频数分布直方图;
(3)求第四组点球各所在40≤x<50的人数占被调查人数的百分比;
(4)若垫球个数在20个以上(含20个)算合格,该校七年级有400名学生,请你估计该校七年级学生在这一项目中合格的学生约有多少人?
 体育课的一个项目是排球30秒对墙垫球,为了解某校七年级学生此项目平时的训练情况,随机抽取了该校部分七年级学生进行测试,根据测试结果,制作了如下尚不完整的频数分布表,其中第1组垫球个数在10≤x<20的人数占被调查人数的10%.
体育课的一个项目是排球30秒对墙垫球,为了解某校七年级学生此项目平时的训练情况,随机抽取了该校部分七年级学生进行测试,根据测试结果,制作了如下尚不完整的频数分布表,其中第1组垫球个数在10≤x<20的人数占被调查人数的10%.| 组别 | 垫球个数x(个) | 频数(人数) |
| 1 | 10≤x<20 | 5 |
| 2 | 20≤x<30 | a |
| 3 | 30≤x<40 | 20 |
| 4 | 40≤x<50 | 16 |
(2)补全频数分布直方图;
(3)求第四组点球各所在40≤x<50的人数占被调查人数的百分比;
(4)若垫球个数在20个以上(含20个)算合格,该校七年级有400名学生,请你估计该校七年级学生在这一项目中合格的学生约有多少人?
4.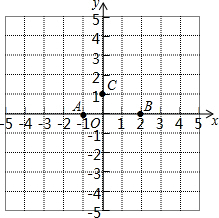 如图,在平面直角坐标系中,以A(-1,0),B(2,0),C(0,1)为顶点构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )
如图,在平面直角坐标系中,以A(-1,0),B(2,0),C(0,1)为顶点构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )
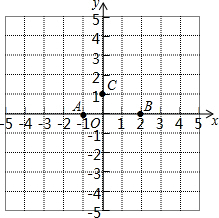 如图,在平面直角坐标系中,以A(-1,0),B(2,0),C(0,1)为顶点构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )
如图,在平面直角坐标系中,以A(-1,0),B(2,0),C(0,1)为顶点构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )| A. | (3,1) | B. | (-4,1) | C. | (1,-1) | D. | (-3,1) |
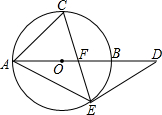 如图,AB为⊙O的直径,点C为$\widehat{AB}$的中点,弦CE交AB于F,过E作⊙O的切线交AB的延长线于D.
如图,AB为⊙O的直径,点C为$\widehat{AB}$的中点,弦CE交AB于F,过E作⊙O的切线交AB的延长线于D.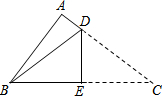 如图,在△ABC中,∠A=90°,AB=6,BC=10,现将△ABC沿折痕DE进行折叠,使顶点C、B重合,则△ABD的周长等于14.
如图,在△ABC中,∠A=90°,AB=6,BC=10,现将△ABC沿折痕DE进行折叠,使顶点C、B重合,则△ABD的周长等于14.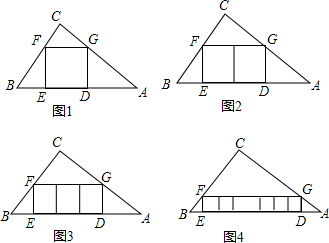
 如图,在Rt△ABO中,∠AOB=90°,点A在第一象限,点B在第二象限,且$\frac{AO}{BO}$=$\frac{1}{\sqrt{5}}$.若点A在y=$\frac{1}{x}$的图象上,则经过点B的反比例函数的解析式是y=-$\frac{5}{x}$.
如图,在Rt△ABO中,∠AOB=90°,点A在第一象限,点B在第二象限,且$\frac{AO}{BO}$=$\frac{1}{\sqrt{5}}$.若点A在y=$\frac{1}{x}$的图象上,则经过点B的反比例函数的解析式是y=-$\frac{5}{x}$.