题目内容
17.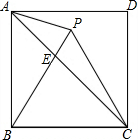 如图,点P在正方形ABCD内,△PBC是正三角形,连接AP、AC,过点P作BC的垂线交AC于点E,若AP=1,则PE=$\frac{\sqrt{6}-\sqrt{2}}{2}$.
如图,点P在正方形ABCD内,△PBC是正三角形,连接AP、AC,过点P作BC的垂线交AC于点E,若AP=1,则PE=$\frac{\sqrt{6}-\sqrt{2}}{2}$.
分析 如图,作PF⊥AE于F.首先证明AP=AE=1,∠PAE=30°,求出PF,EF,利用勾股定理计算即可
解答 解:如图,作PF⊥AE于F.
∵四边形ABCD是正方形,△PBC是等边三角形,
∴∠ABC=90°,∠PBC=60°,AB=BP=BC,∠BAC=45°
∴∠ABP=30°,∠BAP=∠BPA=75°,
∴∠PAE=30°,∠APE=∠AEP=75°,
∴AP=AE=1,PF=$\frac{1}{2}$PA=$\frac{1}{2}$,AF=$\frac{\sqrt{3}}{2}$,
∴EF=1-$\frac{\sqrt{3}}{2}$,
∴PE=$\sqrt{P{F}^{2}+E{F}^{2}}$=$\sqrt{(\frac{1}{2})^{2}+(1-\frac{\sqrt{3}}{2})^{2}}$=$\frac{\sqrt{6}-\sqrt{2}}{2}$.
故答案为$\frac{\sqrt{6}-\sqrt{2}}{2}$.
点评 本题考查等边三角形的性质、正方形的性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
8.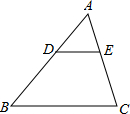 如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,S△ADE:S△ABC=9:49,则EC的长是( )
如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,S△ADE:S△ABC=9:49,则EC的长是( )
 如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,S△ADE:S△ABC=9:49,则EC的长是( )
如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,S△ADE:S△ABC=9:49,则EC的长是( )| A. | 4.5 | B. | 8 | C. | 10.5 | D. | 14 |
12.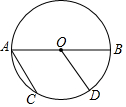 如图,已知AB是⊙O的直径,$\widehat{CD}$=$\widehat{BD}$,则下列结论中正确的是( )
如图,已知AB是⊙O的直径,$\widehat{CD}$=$\widehat{BD}$,则下列结论中正确的是( )
 如图,已知AB是⊙O的直径,$\widehat{CD}$=$\widehat{BD}$,则下列结论中正确的是( )
如图,已知AB是⊙O的直径,$\widehat{CD}$=$\widehat{BD}$,则下列结论中正确的是( )| A. | AC=OD | B. | AC∥OD | C. | $\widehat{AC}$=$\widehat{CD}$ | D. | $\widehat{AC}$=$\widehat{BD}$ |
20.如果+2%表示增加2%,那么-6%表示( )
| A. | 增加14% | B. | 增加6% | C. | 减少6% | D. | 减少26% |
 如图,二次函数y=-$\frac{1}{2}$x2+2的图象与x轴相交于A、B两点,与y相交于点C,点D的横坐标为-1,则:
如图,二次函数y=-$\frac{1}{2}$x2+2的图象与x轴相交于A、B两点,与y相交于点C,点D的横坐标为-1,则: