题目内容
8.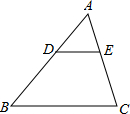 如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,S△ADE:S△ABC=9:49,则EC的长是( )
如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,S△ADE:S△ABC=9:49,则EC的长是( )| A. | 4.5 | B. | 8 | C. | 10.5 | D. | 14 |
分析 先根据相似三角形的性质得出$\frac{AE}{AC}$的值,进而可得出结论.
解答 解:∵DE∥BC,
∴△ADE∽△ABC.
∵S△ADE:S△ABC=9:49,
∴$\frac{AE}{AC}$=$\frac{3}{7}$,即$\frac{6}{AC}$=$\frac{3}{7}$,解得AC=14,
∴EC=14-6=8.
故选B.
点评 本题考查的是相似三角形的判定与性质,熟知相似三角形的对应边成比例是解答此题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
18.等腰三角形的腰长为3,底边长为4,则它的周长为( )
| A. | 7 | B. | 10 | C. | 11 | D. | 10或11 |
13.顺次连接三角形三边的中点,所得的三角形与原三角形对应高的比是( )
| A. | 1:4 | B. | 1:3 | C. | 1:$\sqrt{2}$ | D. | 1:2 |
 如图,△ABC≌△DEF,线段AD=5,DE=3,则BD=2.
如图,△ABC≌△DEF,线段AD=5,DE=3,则BD=2.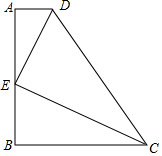 已知:直角梯形ABCD,DE垂直于EC,且AD=1,BC=4,AB=4.
已知:直角梯形ABCD,DE垂直于EC,且AD=1,BC=4,AB=4.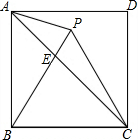 如图,点P在正方形ABCD内,△PBC是正三角形,连接AP、AC,过点P作BC的垂线交AC于点E,若AP=1,则PE=$\frac{\sqrt{6}-\sqrt{2}}{2}$.
如图,点P在正方形ABCD内,△PBC是正三角形,连接AP、AC,过点P作BC的垂线交AC于点E,若AP=1,则PE=$\frac{\sqrt{6}-\sqrt{2}}{2}$.