题目内容
6. 如图,二次函数y=-$\frac{1}{2}$x2+2的图象与x轴相交于A、B两点,与y相交于点C,点D的横坐标为-1,则:
如图,二次函数y=-$\frac{1}{2}$x2+2的图象与x轴相交于A、B两点,与y相交于点C,点D的横坐标为-1,则:(1)点A的坐标为(-2,0),点B的坐标为(2,0),点C的坐标为(0,2),点D的坐标为(-1,$\frac{3}{2}$);
(2)四边形ABCD的面积为$\frac{9}{2}$;
(3)当-3<x<1时,y的取值范围是-$\frac{5}{2}$<y<2.
分析 (1)解方程-$\frac{1}{2}$x2+2=0渴得A、B的坐标;计算自变量为0时所对应的函数值可得到C点坐标,计算自变量为-1时所对应的函数值可得到D点坐标;
(2)连接OD,根据三角形面积公式,利用四边形ABCD的面积=S△OBC+S△OCD+S△OAD进行计算;
(3)先计算当x=-3时,y-$\frac{5}{2}$,然后根据二次函数的性质可得到y的取值范围是-$\frac{5}{2}$<y<2.
解答 解:(1)当y=0时,-$\frac{1}{2}$x2+2=0,解得x1=2,x2=-2,则A(-2,0),B(2,0),
当x=0时,y=-$\frac{1}{2}$x2+2=2,则C(0,2),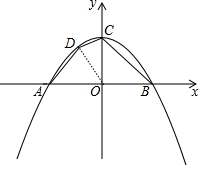
当x=-1时,y=-$\frac{1}{2}$x2+2=-$\frac{1}{2}$+2,则D(0,$\frac{3}{2}$);
(2)连接OD,
四边形ABCD的面积=S△OBC+S△OCD+S△OAD=$\frac{1}{2}$×2×2+$\frac{1}{2}$×2×1+$\frac{1}{2}$×2×$\frac{3}{2}$=$\frac{9}{2}$;
(3)当x=-3时,y=-$\frac{1}{2}$x2+2=-$\frac{5}{2}$,
所以当-3<x<1时,y的取值范围是-$\frac{5}{2}$<y<2.
故答案为(-2,0),(2,0),(0,2),(-1,$\frac{3}{2}$),$\frac{9}{2}$,-$\frac{5}{2}$<y<2.
点评 本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解方程ax2+bx+c=0的问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.下列各组中是同类项的是( )
| A. | 3x2y与2xy2 | B. | $\frac{1}{3}$x4y与$\frac{1}{2}$yx4 | ||
| C. | -2a与0 | D. | $\frac{1}{2}$πa2bc3与-3a2cb3 |
9.下列所列代数式正确的是( )
| A. | a与b的积的立方是ab3 | B. | x与y的平方差是(x-y)2 | ||
| C. | x与y的倒数的差是x-$\frac{1}{y}$ | D. | x与5的差的7倍是7x-5 |
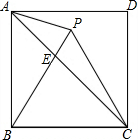 如图,点P在正方形ABCD内,△PBC是正三角形,连接AP、AC,过点P作BC的垂线交AC于点E,若AP=1,则PE=$\frac{\sqrt{6}-\sqrt{2}}{2}$.
如图,点P在正方形ABCD内,△PBC是正三角形,连接AP、AC,过点P作BC的垂线交AC于点E,若AP=1,则PE=$\frac{\sqrt{6}-\sqrt{2}}{2}$.