题目内容
2.把$\frac{1}{ab}$和$\frac{2a-b}{{a}^{2}}$化成分母相同的分式.$\frac{1}{ab}$=$\frac{a}{{a}^{2}b}$
$\frac{2a-b}{{a}^{2}}$=$\frac{2ab{-b}^{2}}{{a}^{2}b}$.
分析 先找出最简公分母a2b,再根据分式的性质进行通分即可.
解答 解:$\frac{1}{ab}$=$\frac{a}{{a}^{2}b}$,
$\frac{2a-b}{{a}^{2}}$=$\frac{2ab{-b}^{2}}{{a}^{2}b}$,
故答案为$\frac{a}{{a}^{2}b}$,$\frac{2ab{-b}^{2}}{{a}^{2}b}$.
点评 本题考查了通分,找出最简分母是解题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
12.抛物线y=-$\frac{1}{2}$(x+2)2与y轴交点坐标为( )
| A. | (0,2) | B. | (0,-2) | C. | (-2,0) | D. | (2,0) |
13.顺次连接三角形三边的中点,所得的三角形与原三角形对应高的比是( )
| A. | 1:4 | B. | 1:3 | C. | 1:$\sqrt{2}$ | D. | 1:2 |
11.下列各组中是同类项的是( )
| A. | 3x2y与2xy2 | B. | $\frac{1}{3}$x4y与$\frac{1}{2}$yx4 | ||
| C. | -2a与0 | D. | $\frac{1}{2}$πa2bc3与-3a2cb3 |
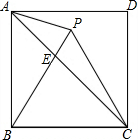 如图,点P在正方形ABCD内,△PBC是正三角形,连接AP、AC,过点P作BC的垂线交AC于点E,若AP=1,则PE=$\frac{\sqrt{6}-\sqrt{2}}{2}$.
如图,点P在正方形ABCD内,△PBC是正三角形,连接AP、AC,过点P作BC的垂线交AC于点E,若AP=1,则PE=$\frac{\sqrt{6}-\sqrt{2}}{2}$.