题目内容
 如图,C是半圆O的直径AB上的一个动点(不与A,B重合),过C作AB的垂线交半圆于点D,以点D,C,O为顶点作矩形DCOE.若AB=10,设AC=x,矩形DCOE的面积为y,写出y与x的函数关系式.
如图,C是半圆O的直径AB上的一个动点(不与A,B重合),过C作AB的垂线交半圆于点D,以点D,C,O为顶点作矩形DCOE.若AB=10,设AC=x,矩形DCOE的面积为y,写出y与x的函数关系式.考点:矩形的性质,函数关系式,圆的认识
专题:
分析:如图,按点C在半径OA或半径OB上两种情况分类讨论;首先运用射影定理求出DC的长度,借助矩形的面积公式即可解决问题.
解答: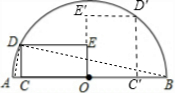 解:如图,当点C在半径OA上时,连接AD、BD;
解:如图,当点C在半径OA上时,连接AD、BD;
∵AB为半圆O的直径,
∴∠ADB=90°,而DC⊥AB,
∴DC2=AC•BC,而AC=x,BC=10-x,
∴DC=
,而OC=5-x,
∴y=(5-x)
;
当点C在半径OB上,即点C′的位置时,
同理可求:y=(x-5)
,
综上所述,y与x的函数关系式为:
y=
.
 解:如图,当点C在半径OA上时,连接AD、BD;
解:如图,当点C在半径OA上时,连接AD、BD;∵AB为半圆O的直径,
∴∠ADB=90°,而DC⊥AB,
∴DC2=AC•BC,而AC=x,BC=10-x,
∴DC=
| -x2+10x |
∴y=(5-x)
| -x2+10x |
当点C在半径OB上,即点C′的位置时,
同理可求:y=(x-5)
| -x2+10x |
综上所述,y与x的函数关系式为:
y=
|
点评:该题主要考查了圆周角定理及其推论、射影定理、矩形的面积公式等几何知识点及其应用问题;作辅助线,牢固掌握圆周角定理及其推论、射影定理等几何知识点是解题的关键.

练习册系列答案
相关题目
 A,B分别为河两岸的两点,其距离不能直接测出,请你根据所学的知识写出一个测量A,B两点之间距离的方法,要求:画出图形,写出已知和求证,并证明.
A,B分别为河两岸的两点,其距离不能直接测出,请你根据所学的知识写出一个测量A,B两点之间距离的方法,要求:画出图形,写出已知和求证,并证明. 已知数轴上一点A对应的数为4.
已知数轴上一点A对应的数为4.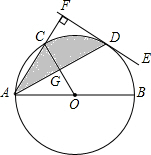 如图,⊙O的直径AB=10,C、D是圆上的两点,且
如图,⊙O的直径AB=10,C、D是圆上的两点,且
 四边形ABCD在平面直角坐标系中的位置,如图所示,已知A(-2,-3),B(2,-2),C(3,1),D(-1,0),求证:四边形ABCD是平行四边形.
四边形ABCD在平面直角坐标系中的位置,如图所示,已知A(-2,-3),B(2,-2),C(3,1),D(-1,0),求证:四边形ABCD是平行四边形. 如图,在△ABC中,D是AC的中点,过A、B、D三点的⊙O交BC于E且点D是弧
如图,在△ABC中,D是AC的中点,过A、B、D三点的⊙O交BC于E且点D是弧 如图,已知?ABCD中,过对角线的交点O的直线交CB,AD的延长线于E和F,证明:BE=DF.
如图,已知?ABCD中,过对角线的交点O的直线交CB,AD的延长线于E和F,证明:BE=DF. 如图,一个楼梯的总长度为5米,总高度为4米,若在楼梯上铺地毯,至少需要多少米?
如图,一个楼梯的总长度为5米,总高度为4米,若在楼梯上铺地毯,至少需要多少米?