Question

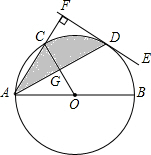如图，⊙O的直径AB=10，C、D是圆上的两点，且

AC

=

CD

=

DB

，设过点D的切线ED交AC于点F，连接OC交AD于点G．
（1）求证：DF⊥AF；
（2）求OG的长；
（3）求阴影部分的面积．

Answer 1

考点：切线的性质,扇形面积的计算

专题：

分析：（1）连接OD，根据

AC

=

CD

=

DB

，可得∠CAD=∠DAB=30°，从而可得AF∥DO，则∠AFD=90°；
（2）根据垂径定理可得OG垂直平分AD，继而可判断OG是△ABD的中位线，在Rt△ABD中求出BD，即可得出OG．
（3）根据S_阴影=S_扇形-S_△ADF即可求得．

解答：解：（1）连接OD，则OD⊥EF，
∵

AC

=

CD

=

DB

，
∴∠CAD=∠DAB=30°，
∵AO=DO，
∴∠OAD=∠ADO，
∴∠FAD=∠ADO，
∴AF∥DO，
∴DF⊥AF．
（2）连接BD，在Rt△ABD中，∠BAD=30°，AB=10，
∴BD=5，
∵

AC

=

CD

，
∴OG垂直平分AD，
∴OG是△ABD的中位线，
∴OG=BD=

5

2

．
（3）连接CD，
∵

AC

=

CD

=

DB

，
∴∠AOC=∠COD=∠DOB=60°，
∵OA=OC=OD=OB，
∴△AOC、△COD、△DOB是等边三角形，
∴AC=CD=OA=

1

2

AB=5，
∵ED是⊙O的切线，
∴∠CDF=∠DAC=30°，
∵DF⊥AF，
∴CF=

1

2

AB=

5

2

，DF=

3

2

AB=

5 3

2

，
∴AF=AC+CF=5+

5

2

=

15

2

∴S_阴影=S_扇形-S_△ADF=

120π×52

360

-

1

2

×

15

2

×

5 3

2

=

25π

3

-

75 3

8

．

点评：本题考查了切线的性质、圆周角定理、垂径定理以及扇形的面积等知识，解答本题要求同学们熟练掌握各定理的内容及含30°角的直角三角形的性质．