题目内容
14. 已知∠BAC=90°,四边形ADEF是正方形且边长为1,则$\frac{1}{AB}$+$\frac{1}{BC}$+$\frac{1}{CA}$的最大值为1+$\frac{\sqrt{2}}{4}$,简述理由(可列式):$\frac{1}{AB}$+$\frac{1}{BC}$+$\frac{1}{CA}$的最大值=1+$\frac{\sqrt{2}}{4}$.
已知∠BAC=90°,四边形ADEF是正方形且边长为1,则$\frac{1}{AB}$+$\frac{1}{BC}$+$\frac{1}{CA}$的最大值为1+$\frac{\sqrt{2}}{4}$,简述理由(可列式):$\frac{1}{AB}$+$\frac{1}{BC}$+$\frac{1}{CA}$的最大值=1+$\frac{\sqrt{2}}{4}$.
分析 由四边形ADEF是正方形,得到AD=AF=1,DE∥AC,AD∥EF,于是得到$\frac{1}{AB}$+$\frac{1}{BC}$+$\frac{1}{CA}$=1+$\frac{1}{BC}$,由勾股定理得到BC2=(BD+1)2+(CF+1)2=BD2+CF2+2(BD+CF)+2,根据全平方公式得到BC2=BD2+CF2+2(BD+CF)+2≥2BD•CF+4$\sqrt{BD•CF}$+2,根据相似三角形的性质得到BD•CF=1,于是得到BC的最小值=2$\sqrt{2}$,即可得到结论.
解答 解:1+$\frac{\sqrt{2}}{4}$;理由:
∵四边形ADEF是正方形,
∴AD=AF=1,DE∥AC,AD∥EF,
∴$\frac{AD}{AB}=\frac{CE}{BC},\frac{AF}{AC}=\frac{BE}{BC}$,
∴$\frac{1}{AB}$+$\frac{1}{BC}$+$\frac{1}{CA}$=$\frac{AD}{AB}+\frac{AF}{AC}+\frac{1}{BC}$=$\frac{CE}{BC}+\frac{BE}{BC}$+$\frac{1}{BC}$=1+$\frac{1}{BC}$,
∵BC2=(BD+1)2+(CF+1)2=BD2+CF2+2(BD+CF)+2,
∵BD2+CF2≥2BD•CF,BD+CF=$\sqrt{(BD+CF)^{2}}$=$\sqrt{B{D}^{2}+C{F}^{2}+2BD•CF}$$≥\sqrt{4BD•CF}$,
∴BC2=BD2+CF2+2(BD+CF)+2≥2BD•CF+4$\sqrt{BD•CF}$+2,
∵△BDE∽△EFC,
∴$\frac{BD}{EF}=\frac{DE}{CF}$,
∴BD•CF=1,
BC2≥2+2BD•CF+$4\sqrt{BD•CF}$=8,
∴BC的最小值=2$\sqrt{2}$,
∴$\frac{1}{AB}$+$\frac{1}{BC}$+$\frac{1}{CA}$的最大值=1+$\frac{\sqrt{2}}{4}$.
故答案为:1+$\frac{\sqrt{2}}{4}$,$\frac{1}{AB}$+$\frac{1}{BC}$+$\frac{1}{CA}$的最大值=1+$\frac{\sqrt{2}}{4}$.
点评 本题考查了相似三角形的判定和性质,正方形的性质,平行线分线段成比例定理,完全平方公式,证得BC2≥2+2BD•CF+$4\sqrt{BD•CF}$=8是解题的关键.

| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b>0 | D. | k<0,b<0 |
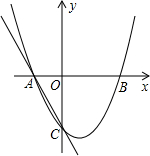 如图,抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(2,0)两点,与y轴交于点C(0,-2),过A、C画直线.
如图,抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(2,0)两点,与y轴交于点C(0,-2),过A、C画直线.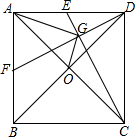 已知如图,正方形ABCD的对角线AC、BD交于O,点E、F分别是AD、AB边的中点,连接DF、CE交于点G,连接AG、OG.若AD=2,则OG=$\frac{\sqrt{10}}{5}$.
已知如图,正方形ABCD的对角线AC、BD交于O,点E、F分别是AD、AB边的中点,连接DF、CE交于点G,连接AG、OG.若AD=2,则OG=$\frac{\sqrt{10}}{5}$.