题目内容
8.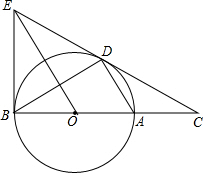 如图,D为⊙O上一点,点C在直线BA的延长线上,且∠CDA=∠CBD.
如图,D为⊙O上一点,点C在直线BA的延长线上,且∠CDA=∠CBD.(1)求证:CD是⊙O的切线;
(2)若BC=8cm,tan∠CDA=$\frac{1}{2}$,求⊙O的半径;
(3)在(2)条件下,过点B作⊙O的切线交CD的延长线于点E,连接OE,求四边形OEDA的面积.
分析 (1)要证明CD是⊙O的切线,只需要连接OD,证明∠ODC=90°即可,由∠CDA=∠CBD,∠BDA=90°,OA=OD得到∠ODA=∠OAD,然后进行转化即可得到∠ODC=90°,本题得以解决;
(2)根据题意可以得到△CDA和△CBD相似,然后根据BC=8cm,tan∠CDA=$\frac{1}{2}$,∠CDA=∠CBD,可以求得CD、CA的长,从而可以求得BA的长,进而可以得到⊙O的半径;
(3)由题意可得,∠EBC=90°,可以证明△EBC和△ODC相似,从而可以求得EB的长,然后根据四边形OEDA的面积等于△EBC的面积减去△EBO的面积再减去△DAC的面积,从而可以得到四边形OEDA的面积,本题得以解决.
解答 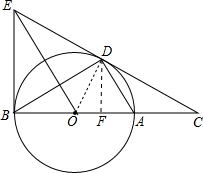 (1)证明:连接OD,如右图所示,
(1)证明:连接OD,如右图所示,
∵AB为⊙O的直径,
∴∠BDA=90°,
又∵OD=OA,∠CDA=∠CBD,
∴∠ODA=∠OAD,
∴∠CBD+∠OAD=180°-∠BDA=90°,
∴∠ODA+∠CDA=∠OAD+∠CDA=90°,
∴∠ODC=90°,
即CD是⊙O的切线;
(2)解:∵∠DCA=∠BCD,∠CDA=∠CBD,
∴△CDA∽△CBD,
∴$\frac{CD}{CB}=\frac{CA}{CD}=\frac{DA}{BD}$,
又∵BC=8cm,tan∠CDA=$\frac{1}{2}$,∠CDA=∠CBD,∠BDA=90°,
∴tan∠CBD=$\frac{DA}{BD}=\frac{1}{2}$,
∴$\frac{CD}{CB}=\frac{CA}{CD}=\frac{DA}{BD}$=$\frac{1}{2}$,
∴$\frac{CD}{8}=\frac{CA}{CD}=\frac{1}{2}$,
解得,CD=4,CA=2,
∴BA=CB-CA=8-2=6,
∴OB=3,
即⊙O的半径是3cm;
(3)作DF⊥BC于点F,如右上图所示
由已知可得,∠ODC=∠EBC=90°,∠DCO=∠BCE,
∴△DCO∽△BCE,
∴$\frac{OD}{EB}=\frac{CD}{CB}$,
∵OD=3,CD=4,CB=8,
∴EB=6,
又∵CO=CB-OB=8-3=5,OD=3,CD=4,∠ODC=90°,DF⊥OC,
∴$\frac{CO•DF}{2}=\frac{OD•CD}{2}$,
解得DF=2.4,
∴S四边形OEDA=S△EBC-S△EBO-S△DAC=$\frac{BC•EB}{2}-\frac{EB•OB}{2}-\frac{CA•DF}{2}$=$\frac{8×6}{2}-\frac{6×3}{2}-\frac{2×2.4}{2}=12.6c{m}^{2}$,
即四边形OEDA的面积是12.6cm2.
点评 本题考查切线的判定、锐角三角函数、相似三角形的性质、切线的性质、面积法中割补法的应用,解题的关键是明确题意,作出合适的辅助线,画出相应的图形,找出所求问题需要的条件,运用数形结合的思想解答问题.

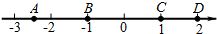 如图,数轴上有A、B、C、D四点,其中表示互为相反数的两个实数所对应的点是( )
如图,数轴上有A、B、C、D四点,其中表示互为相反数的两个实数所对应的点是( )| A. | 点A与点D | B. | 点A与点C | C. | 点B与点D | D. | 点B与点C |
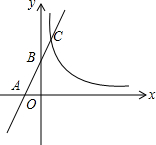 如图,已知直线与x轴、y轴分别交于A、B两点,且与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限交于点C,若AB=BC,AB=2OA=2.
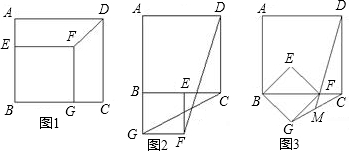
如图,已知直线与x轴、y轴分别交于A、B两点,且与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限交于点C,若AB=BC,AB=2OA=2.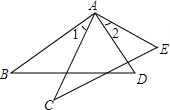 如图,AD=AE,∠B=∠C,∠1=∠2,求证:△ABD≌△ACE.
如图,AD=AE,∠B=∠C,∠1=∠2,求证:△ABD≌△ACE.