题目内容
9.解下列三元一次方程组:(1)$\left\{\begin{array}{l}{x-4y+z=-3}\\{2x+y-z=18}\\{x-y-z=7}\end{array}\right.$
(2)$\left\{\begin{array}{l}{x:y:z=2:3:5}\\{x+y+z=100}\end{array}\right.$.
分析 (1)①+②得出x-y=5④,②-③得出x+2y=11⑤,由④和⑤组成方程组,求出方程组的解,再求出z即可;
(2)设x=2k,y=3k,z=5k,代入方程x+y+z=100得出10k=100,求出k,即可求出方程组的解.
解答 解:(1)$\left\{\begin{array}{l}{x-4y+z=-3①}\\{2x+y-z=18②}\\{x-y-z=7③}\end{array}\right.$
①+②得:3x-3y=15,
x-y=5④,
②-③得:x+2y=11⑤,
由④和⑤组成方程组:$\left\{\begin{array}{l}{x-y=5}\\{x+2y=11}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=7}\\{y=2}\end{array}\right.$,
把$\left\{\begin{array}{l}{x=7}\\{y=2}\end{array}\right.$代入③得:7-2-z=7,
解得:z=-2,
所以原方程组的解为:$\left\{\begin{array}{l}{x=7}\\{y=2}\\{z=-2}\end{array}\right.$;
(2)设x=2k,y=3k,z=5k,
代入方程x+y+z=100得:10k=100,
解得:k=10,
即x=20,y=30,z=50,
所以原方程组的解为:$\left\{\begin{array}{l}{x=20}\\{y=30}\\{z=50}\end{array}\right.$.
点评 本题考查了解三元一次方程组,能把三元一次方程组转化成二元一次方程组或一元一次方程是解此题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
4.若反比例函数y=-$\frac{4}{x}$的图象经过第二象限的点(a,-a),则a的值为( )
| A. | 2或-2 | B. | -2 | C. | 2 | D. | 4 |
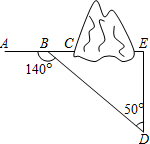 如图,在某隧道建设工程中,需沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工,为了使开挖点E在直线AC上,现在AC上取一点B,AC外取一点D,测得∠ABD=140°,BD=704m,∠D=50°,求开挖点E到点D的距离.(结果精确到1米)
如图,在某隧道建设工程中,需沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工,为了使开挖点E在直线AC上,现在AC上取一点B,AC外取一点D,测得∠ABD=140°,BD=704m,∠D=50°,求开挖点E到点D的距离.(结果精确到1米)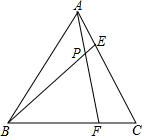 如图,在等边△ABC中,点F、E分别在BC、AC边上,AE=CF,AF与BE相交于点P.
如图,在等边△ABC中,点F、E分别在BC、AC边上,AE=CF,AF与BE相交于点P.