题目内容
11.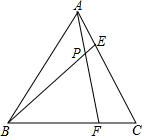 如图,在等边△ABC中,点F、E分别在BC、AC边上,AE=CF,AF与BE相交于点P.
如图,在等边△ABC中,点F、E分别在BC、AC边上,AE=CF,AF与BE相交于点P.(1)求证:△AEP∽△BEA;
(2)若BE=3AE,AP=2,求等边△ABC的边长.
分析 (1)根据等边三角形的性质得到AB=AC,∠C=∠CAB=60°,根据全等三角形的性质得到∠ABE=∠CAF,于是得到结论;
(2)根据相似三角形的性质即可得到结论.
解答 (1)证明:∵△ABC为等边三角形,
∴AB=AC,∠C=∠CAB=60°,
又∵AE=CF,
在△ABE和△CAF中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠ACF}\\{AE=CF}\end{array}\right.$,
∴△ABE≌△CAF(SAS),
∴∠ABE=∠CAF,
∵∠AEB=∠BEA,
∴△AEP∽△BEA;
(2)解:∵△AEP∽△BEA,
∴$\frac{AE}{BE}=\frac{AP}{AB}$,
∵BE=3AE,AP=2,
∴AB=6,
∴等边△ABC的边长是6.
点评 本题考查了等边三角形性质,全等三角形的判定与性质,以及相似三角形的判定及性质的应用,解答本题的关键是注意转化思想的运用.

练习册系列答案
相关题目
2.下列说法正确的是( )
| A. | 任何数都有算术平方根 | B. | 只有正数有算术平方根 | ||
| C. | 0和正数都有算术平方根 | D. | 负数有算术平方根 |
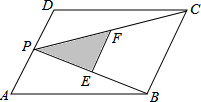 如图,P是平行四边形ABCD边AD上一动点,点E,F分别为PC,PB的中点,对于下列各值:
如图,P是平行四边形ABCD边AD上一动点,点E,F分别为PC,PB的中点,对于下列各值: 如图,已知AB⊥BC,FC⊥BC,AB=BC,点E在BC上,AE⊥BF,垂足为G.求证:AE=BF.
如图,已知AB⊥BC,FC⊥BC,AB=BC,点E在BC上,AE⊥BF,垂足为G.求证:AE=BF.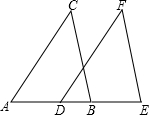 如图,点A,D,B,E在同一条直线上,AC=DF,BC=EF,∠C=∠F.
如图,点A,D,B,E在同一条直线上,AC=DF,BC=EF,∠C=∠F.