题目内容
在第19个“4.23世界读书日”到来之际,某校举办了“中国梦•我的梦”征文比赛,从同学们的投稿中分别评出一等奖、二等奖、三等奖和优秀奖,并将获奖结果绘制成如下两幅不完整的统计图:

(1)这次征文比赛一共有 名学生获奖,请把条形统计图补充完整;
(2)在这次征文比赛获得一等奖的同学中,初一、初二年级各有一名学生,其余全是初三年级学生,现准备从获得一等奖的同学中随机邀请两名学生发表获奖感言,请你用列表成画树状图的方法,求出所选两名学生恰好都来自初三年级的概率.

(1)这次征文比赛一共有
(2)在这次征文比赛获得一等奖的同学中,初一、初二年级各有一名学生,其余全是初三年级学生,现准备从获得一等奖的同学中随机邀请两名学生发表获奖感言,请你用列表成画树状图的方法,求出所选两名学生恰好都来自初三年级的概率.
考点:列表法与树状图法,扇形统计图,条形统计图
专题:
分析:(1)根据三等奖的人数以及三等奖所占的百分比即可求出这次征文比赛一共有多少名学生获奖;
(2)首先求出获得一等奖的学生人数,再用列表法或树形图法列举出所有可能的结果,利用求概率公式计算即可.
(2)首先求出获得一等奖的学生人数,再用列表法或树形图法列举出所有可能的结果,利用求概率公式计算即可.
解答:解:(1)由题意可知:这次征文比赛一共有12÷
×100%=40名学生获奖;
故答案为:40;
条形统计图补充如图所示:
(2)由(1)可知获得一等奖的学生共有40-18-12-6=4人,
设初一为白,初二为黄,初三分别为红1,红2,
根据题意画出树状图如下:

一共有12种情况,所以所选两名学生恰好都来自初三年级的概率为
=
| 108 |
| 360 |
故答案为:40;

条形统计图补充如图所示:
(2)由(1)可知获得一等奖的学生共有40-18-12-6=4人,
设初一为白,初二为黄,初三分别为红1,红2,
根据题意画出树状图如下:

一共有12种情况,所以所选两名学生恰好都来自初三年级的概率为
| 2 |
| 12 |
| 1 |
| 6 |
点评:本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
已知x1,x2是关于x的一元二次方程x2-2x-a=0的两个实数根,且x12+x22+3x1x2=5,则a的值是( )
| A、2 | B、-2 | C、1 | D、-1 |
 如图:⊙M在直角坐标系中,圆心M在y轴正半轴上,弧AB所对的圆心角是120°,⊙M的半径是2cm.
如图:⊙M在直角坐标系中,圆心M在y轴正半轴上,弧AB所对的圆心角是120°,⊙M的半径是2cm. 如图,⊙O的圆内接四边形ABCD中,AC是直径,且AD=CD,AB=8,BD=10
如图,⊙O的圆内接四边形ABCD中,AC是直径,且AD=CD,AB=8,BD=10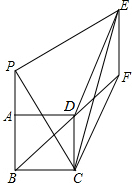 已知正方形ABCD,点P为射线BA上的一点(不和点A、B重合),过P作PE⊥CP,且CP=PE,过E作EF∥CD交射线BD于F.若△EFC的面积与四边形PEFC的面积之比为3:20,则tan∠BPC=
已知正方形ABCD,点P为射线BA上的一点(不和点A、B重合),过P作PE⊥CP,且CP=PE,过E作EF∥CD交射线BD于F.若△EFC的面积与四边形PEFC的面积之比为3:20,则tan∠BPC=