Question

14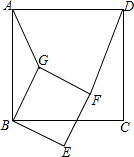．如图，在平面内，四边形ABCD和BEFG均为正方形，则AG：DF：CE=1：$\sqrt{2}$：1．

Answer 1

分析 连接BD、BF，可证明△ABG∽△DBF，可求得AG：DF，连接CE，可证明△ABG≌△CBE，可求得AG=CE，可求得答案．

解答 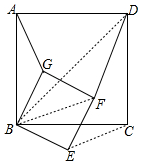解：
连接BD、BF和CE，
∵四边形ABCD和BEFG均为正方形，
∴$\frac{AB}{BD}$=$\frac{BG}{BF}$=$\frac{1}{\sqrt{2}}$，且∠ABD=∠GBF=45°，
∴∠ABG+∠GBD=∠GBD+∠DBF，
∴∠ABG=∠GBD，
∴△ABG∽△DBF，
∴$\frac{AG}{DF}$$\frac{1}{\sqrt{2}}$，
又∴AB=BC，BG=BE，∠ABC=∠GBE=90°，
∴∠AGB+∠GBC=∠GBC+∠CBE，
∴∠AGB=∠CBE，
在△ABG和△CBE中
$\left\{\begin{array}{l}{AB=BC}\\{∠ABG=∠CBE}\\{BG=BE}\end{array}\right.$
∴△ABG≌△CBE（SAS），
∴AG=CE，
∴AG：CE=1：1，
∴AG：DF：CE=1：$\sqrt{2}$：1，
故答案为：1：$\sqrt{2}$：1．

点评 本题主要考查相似三角形和全等三角形的判定和性质，构造全等或相似三角形是解题的关键．