题目内容
6．若|3x+2y-4|与（5x+7y-3）2互为相反数，则x+y=1．分析 根据互为相反数两数之和为0列出关系式，再利用非负数的性质求出x与y的值，即可求出x+y的值．
解答 解：∵|3x+2y-4|+（5x+7y-3）2=0，
∴$\left\{\begin{array}{l}{3x+2y=4①}\\{5x+7y=3②}\end{array}\right.$，
①×7-②×2得：11x=22，即x=2，
把x=2代入①得：y=-1，
则x+y=2-1=1．
故答案为：1
点评 此题考查了解二元一次方程组，以及非负数的性质，熟练掌握运算法则是解本题的关键．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
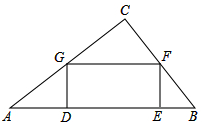如图，在直角三角形ABC中，∠C=90°，AC=3，BC=4，矩形DEFG内接于△ABC中，如果DG：DE=3：5，求矩形DEFG的周长．
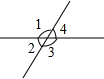如图，如果∠1=120°，则∠2=60°．
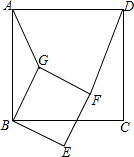如图，在平面内，四边形ABCD和BEFG均为正方形，则AG：DF：CE=1：$\sqrt{2}$：1．
11．
一个不等式的解如图所示，则此不等式可能是（ ）
一个不等式的解如图所示，则此不等式可能是（ ）| A． | $\frac{x+4}{x-2}$≤0 | B． | $\frac{x+2}{x-4}$≤0 | C． | $\frac{x-4}{x+2}$≤0 | D． | （x-4）（x+2）≤0 |
