题目内容
2.若函数y=x2+ax+1(0<x<$\frac{1}{2}$)的图象恒在x轴的上方,则a的最小值是( )| A. | 0 | B. | -2 | C. | -3 | D. | -$\frac{5}{2}$ |
分析 根据函数y=x2+ax+1(0<x<$\frac{1}{2}$)的图象恒在x轴的上方可知当x=$\frac{1}{2}$时,y≥0,得到a的不等式,求出最值即可.
解答 解:∵函数y=x2+ax+1(0<x<$\frac{1}{2}$)的图象恒在x轴的上方,
∴当x=$\frac{1}{2}$时,y≥0,
∴$\frac{1}{4}$+$\frac{1}{2}$a+1≥0,
∴a≥-$\frac{5}{2}$,
即a的最小值为-$\frac{5}{2}$,
故选D.
点评 本题主要考查了抛物线与x轴的交点,解题的关键是根据题意可知当x=$\frac{1}{2}$时,y≥0,此题难度不大.

练习册系列答案
相关题目
11. 一个不等式的解如图所示,则此不等式可能是( )
一个不等式的解如图所示,则此不等式可能是( )
 一个不等式的解如图所示,则此不等式可能是( )
一个不等式的解如图所示,则此不等式可能是( )| A. | $\frac{x+4}{x-2}$≤0 | B. | $\frac{x+2}{x-4}$≤0 | C. | $\frac{x-4}{x+2}$≤0 | D. | (x-4)(x+2)≤0 |
 如图,在△ABC中,BC边上的高是AD;在△ACD中,CD边上的高是AD;以CF为高的三角形是△BCF,△ABC.
如图,在△ABC中,BC边上的高是AD;在△ACD中,CD边上的高是AD;以CF为高的三角形是△BCF,△ABC.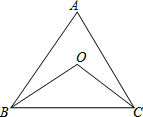 如图,点O是△ABC的∠ABC、∠ACB的平分线的交点,若∠A为锐角,∠BOC=α°,则α的取值范围为90°<α<135°.
如图,点O是△ABC的∠ABC、∠ACB的平分线的交点,若∠A为锐角,∠BOC=α°,则α的取值范围为90°<α<135°.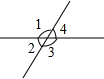 如图,如果∠1=120°,则∠2=60°.
如图,如果∠1=120°,则∠2=60°.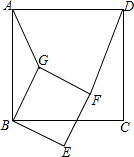 如图,在平面内,四边形ABCD和BEFG均为正方形,则AG:DF:CE=1:$\sqrt{2}$:1.
如图,在平面内,四边形ABCD和BEFG均为正方形,则AG:DF:CE=1:$\sqrt{2}$:1.