题目内容
4.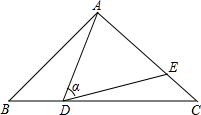 如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=$\frac{4}{5}$.下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8;④0<CE≤6.4.其中正确的结论是①②④.(把你认为正确结论的序号都填上)
如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=$\frac{4}{5}$.下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8;④0<CE≤6.4.其中正确的结论是①②④.(把你认为正确结论的序号都填上)
分析 作AH⊥BC于H,如图,根据等腰三角形的性质易得∠B=∠ADE=∠C,于是可判断△ADE∽△ACD;在Rt△ABH中,利用三角函数的定义可计算出BH=8,则BC=2BH=16,所以当BD=6,则CD=10=AB,再证明∠EDC=∠BAD,则可判断△ABD≌△DCE;先证明△ABD∽△DCE,分类讨论:当∠DEC=90°,则∠ADB=90°,可得BD为8;当∠EDC=90°,则∠BAD=90°,根据三角函数定义可得BD=$\frac{AB}{cosα}$=$\frac{25}{2}$;设BD=x,则CD=16-x,由△ABD∽△DCE,利用相似比可得CE=-$\frac{1}{10}$(x-8)2+6.4,然后根据二次函数的性质可得CE的最大值为6.4,于是有0<CE≤6.4.
解答 解:作AH⊥BC于H,如图,
∵AB=AC,
∴∠B=∠C=α,BH=CH,
而∠ADE=∠B=α,
∴∠ADE=∠C,
而∠DAE=∠CAD,
∴△ADE∽△ACD,所以①正确;
在Rt△ABH中,cosB=$\frac{BH}{AB}$,
∴BH=10×$\frac{4}{5}$=8,
∴BC=2BH=16,
当BD=6,则CD=10,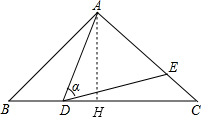
∵∠ADC=∠B+∠BAD,
而∠ADE=∠B=α,
∴∠EDC=∠BAD,
在△ABD与△DCE中
$\left\{\begin{array}{l}{∠B=∠C}\\{AB=DC}\\{∠BAD=∠CDE}\end{array}\right.$,
∴△ABD≌△DCE,所以②正确;
∵∠B=∠C,∠BAD=∠CDE,
∴△ABD∽△DCE,
△DCE为直角三角形,当∠DEC=90°,则∠ADB=90°,BD为8;当∠EDC=90°,则∠BAD=90°,BD=$\frac{AB}{cosα}$=$\frac{25}{2}$,所以③错误;
设BD=x,则CD=16-x,
由△ABD∽△DCE得$\frac{BD}{CE}$=$\frac{AB}{DC}$,即$\frac{x}{CE}$=$\frac{10}{10-x}$,
∴CE=-$\frac{1}{10}$(x-8)2+6.4,
∴CE的最大值为6.4,
∴0<CE≤6.4,所以④正确.
故答案为①②④.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;或依据基本图形对图形进行分解、组合.

 名校课堂系列答案
名校课堂系列答案| A. | M≥N | B. | M>N | C. | M≤N | D. | M<N |
| A. | 5 | B. | 4 | C. | 3 | D. | 1 |
| A. | 扩大3倍 | B. | 不变 | C. | 缩小3倍 | D. | 缩小6倍 |
| A. |  | B. |  | C. |  | D. |  |
| A. | k≥-2 | B. | k≤-2 | C. | k≥2 | D. | k≤2 |

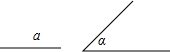 (1)已知:线段a,∠α.求作:△ABC,使BC=a,∠C=∠B=∠α.(不写作法,保留作图痕迹)
(1)已知:线段a,∠α.求作:△ABC,使BC=a,∠C=∠B=∠α.(不写作法,保留作图痕迹)