题目内容
9.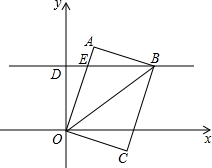 如图,在平面直角坐标系中,有一矩形OABC,OA=8,OC=6,过点D(0,6)作y轴的垂线交OA于点E,点B恰在这条直线上.
如图,在平面直角坐标系中,有一矩形OABC,OA=8,OC=6,过点D(0,6)作y轴的垂线交OA于点E,点B恰在这条直线上.(1)求矩形OABC的对角线的长;
(2)求点B的坐标;
(3)求△EOB的面积.
分析 (1)由矩形的性质得出AB=OC=6,∠A=90°,由勾股定理求出OB即可;
(2)由勾股定理求出BD,即可得出结果;
(3)由HL证明Rt△OBD≌Rt△BOA,得出∠OBD=∠BOA,证出OE=BE,设OE=BE=x,则DE=8-x,在Rt△ODE中,由勾股定理得出方程,解方程求出BE,即可得出结果.
解答 解:(1)∵四边形OABC是矩形,
∴AB=OC=6,∠A=90°,
∴OB=$\sqrt{O{A}^{2}+A{B}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10,
即矩形OABC的对角线的长为10;
(2)∵BD⊥OD,
∴∠ODB=90°,
∴BD=$\sqrt{O{B}^{2}-O{D}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴点B的坐标为(8,6);
(3)∵OD=6,AB=6,
∴OD=AB,
在Rt△OBD和Rt△BOA中,$\left\{\begin{array}{l}{OB=BO}\\{OD=BA}\end{array}\right.$,
∴Rt△OBD≌Rt△BOA(HL),
∴∠OBD=∠BOA,
∴OE=BE,
设OE=BE=x,则DE=8-x,
在Rt△ODE中,由勾股定理得:62+(8-x)2=x2,
解得:x=$\frac{25}{4}$,即BE=$\frac{25}{4}$,
∴△EOB的面积=$\frac{1}{2}$BE•OD=$\frac{1}{2}$×$\frac{25}{4}$×6=$\frac{75}{4}$.
点评 本题考查了矩形的性质、勾股定理、坐标与图形性质、全等三角形的判定与性质、等腰三角形的判定;熟练掌握矩形的性质,证出BE=OE,由勾股定理得出方程是解决问题(3)的关键.

练习册系列答案
相关题目
20.如果一个角的补角是110°,则这个角的余角的度数是( )
| A. | 30° | B. | 20° | C. | 70° | D. | 110° |
14.已知四点A(0,-2),B(1,0),C(2,2),D(0,4),若一个二次函数的图象经过这四点中的三点,则这个二次函数图象的对称轴为( )
| A. | x=$\frac{7}{6}$ | B. | x=-$\frac{7}{6}$ | C. | x=-$\frac{6}{7}$ | D. | x=$\frac{6}{7}$ |
19.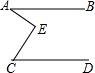 如图,已知直线AB∥CD,∠A=20°,∠C=40°,则∠E=( )
如图,已知直线AB∥CD,∠A=20°,∠C=40°,则∠E=( )
 如图,已知直线AB∥CD,∠A=20°,∠C=40°,则∠E=( )
如图,已知直线AB∥CD,∠A=20°,∠C=40°,则∠E=( )| A. | 20° | B. | 40° | C. | 60° | D. | 80° |
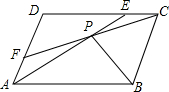 ?ABCD中,E、F分别是CD、AD边上的点,且AE=CF,AE,CF交于点P,求证:PB平分∠APC.
?ABCD中,E、F分别是CD、AD边上的点,且AE=CF,AE,CF交于点P,求证:PB平分∠APC. 已知:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.
已知:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D. 如图,在矩形ABCD中,BC=2AB.以点B为圆心,BC长为半径作弧交AD于点E,连结BE.若AB=1,则DE的长为2-$\sqrt{3}$.
如图,在矩形ABCD中,BC=2AB.以点B为圆心,BC长为半径作弧交AD于点E,连结BE.若AB=1,则DE的长为2-$\sqrt{3}$.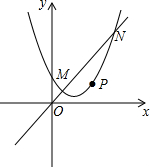 如图,抛物线y=ax2+bx+c(a≠0)与直线y=kx(k≠0)相交于点M(1,1),N(3,3),且这条抛物线的对称轴为x=1.
如图,抛物线y=ax2+bx+c(a≠0)与直线y=kx(k≠0)相交于点M(1,1),N(3,3),且这条抛物线的对称轴为x=1.