题目内容
18.计算:(1)($\frac{1}{3}$)-2÷(-$\frac{2}{3}$)0+(-2)3;
(2)(2a-3b)2-4a(a-3b).
(3)分解因式:m4-2m2+1.
(4)解方程组$\left\{\begin{array}{l}{x-y=-2}\\{3x+2y=4}\end{array}\right.$.
(5)先化简,再求值:4x(x-1)-(2x+1)(2x-1),其中x=-1.
分析 (1)分别根据0指数幂及负整数指数幂的计算法则、数的乘方法则计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先去括号,再合并同类项即可;
(3)根据完全平方公式与平方差公式把原式进行因式分解即可;
(4)先利用加减消元法求出x的值,再用代入消元法求出y的值即可;
(5)先根据整式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:(1)原式=9÷1+(-8)
=9-8
=1;
(2)原式=4a2-12ab+9b2-4a2+12ab
=9b2;
(3)原式=(m2-1)2=(m+1)2(m-1)2.
(4)$\left\{\begin{array}{l}x-y=-2①\\ 3x+2y=4②\end{array}\right.$,
①×2+②得:5x=0,即x=0,
把x=0代入①得:y=2,
则方程组的解为$\left\{\begin{array}{l}x=0\\ y=2\end{array}\right.$;
(5)原式=4x2-4x-4x2+1
=-4x+1,
当x=-1时,原式=4+1=5.
点评 本题考查的是解二元一次方程组,熟知解二元一次方程组的加减消元法和代入消元法是解答此题的关键.

练习册系列答案
相关题目
7.如果代数式$\frac{\sqrt{x}}{\sqrt{x-1}}$有意义,那么x的取值范围是( )
| A. | x≥0 | B. | x≠1 | C. | x>1 | D. | x≥0且 x≠1 |
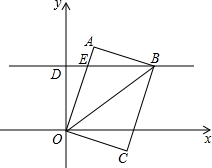 如图,在平面直角坐标系中,有一矩形OABC,OA=8,OC=6,过点D(0,6)作y轴的垂线交OA于点E,点B恰在这条直线上.
如图,在平面直角坐标系中,有一矩形OABC,OA=8,OC=6,过点D(0,6)作y轴的垂线交OA于点E,点B恰在这条直线上.
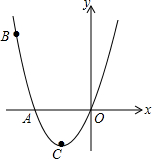 如图,已知抛物线经过点A(-2,0),B(-3,3)及原点O,顶点为C.
如图,已知抛物线经过点A(-2,0),B(-3,3)及原点O,顶点为C.