题目内容
19.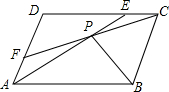 ?ABCD中,E、F分别是CD、AD边上的点,且AE=CF,AE,CF交于点P,求证:PB平分∠APC.
?ABCD中,E、F分别是CD、AD边上的点,且AE=CF,AE,CF交于点P,求证:PB平分∠APC.
分析 连接BF、BE,作BM⊥CF,BN⊥AE垂足分别为M、N,根据S△ABE=$\frac{1}{2}$S平行四边形ABCD,S△BCF=$\frac{1}{2}$S平行四边形ABCD先证明S△ABE=S△BCF,可以得到BM=BN,由此可以解决问题.
解答 证明:如图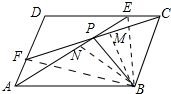 连接BF、BE,作BM⊥CF,BN⊥AE垂足分别为M、N.
连接BF、BE,作BM⊥CF,BN⊥AE垂足分别为M、N.
∵四边形ABCD是平行四边形,
∴AD∥BC,CD∥AB,
∴S△ABE=$\frac{1}{2}$S平行四边形ABCD,S△BCF=$\frac{1}{2}$S平行四边形ABCD,
∴S△ABE=S△BCF,
∴$\frac{1}{2}$•AE•BN=$\frac{1}{2}$•CF•BM,
∵AE=CF,
∴BM=BN,
∴PB平分∠APC.
点评 本题考查平行四边形的性质、三角形的面积公式,角平分线的判定定理等知识,解题的关键添加辅助线以及△ABE和△BCF面积相等的证明,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.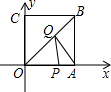 如图所示,四边形OABC是正方形,边长为4,点A、C分别在x轴、y轴的正半轴上,点P在OA上,且P点的坐标为(3,0),Q是OB上一动点,则PQ+AQ的最小值为( )
如图所示,四边形OABC是正方形,边长为4,点A、C分别在x轴、y轴的正半轴上,点P在OA上,且P点的坐标为(3,0),Q是OB上一动点,则PQ+AQ的最小值为( )
 如图所示,四边形OABC是正方形,边长为4,点A、C分别在x轴、y轴的正半轴上,点P在OA上,且P点的坐标为(3,0),Q是OB上一动点,则PQ+AQ的最小值为( )
如图所示,四边形OABC是正方形,边长为4,点A、C分别在x轴、y轴的正半轴上,点P在OA上,且P点的坐标为(3,0),Q是OB上一动点,则PQ+AQ的最小值为( )| A. | 5 | B. | $\sqrt{10}$ | C. | 4 | D. | 6 |
7.若a=$\sqrt{2}$,b=$\sqrt{7}$-$\sqrt{3}$,c=$\sqrt{6}$-$\sqrt{2}$,则a,b,c的大小关系是( )
| A. | c<a<b | B. | b<c<a | C. | c<b<a | D. | b<a<c |
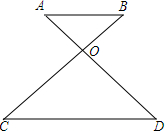 如图,OA:OD=OB:OC=1:2,OB=3.
如图,OA:OD=OB:OC=1:2,OB=3. 如图,在平面直角坐标系中,有一矩形OABC,OA=8,OC=6,过点D(0,6)作y轴的垂线交OA于点E,点B恰在这条直线上.
如图,在平面直角坐标系中,有一矩形OABC,OA=8,OC=6,过点D(0,6)作y轴的垂线交OA于点E,点B恰在这条直线上.