题目内容
4. 如图,在矩形ABCD中,BC=2AB.以点B为圆心,BC长为半径作弧交AD于点E,连结BE.若AB=1,则DE的长为2-$\sqrt{3}$.
如图,在矩形ABCD中,BC=2AB.以点B为圆心,BC长为半径作弧交AD于点E,连结BE.若AB=1,则DE的长为2-$\sqrt{3}$.
分析 根据矩形的性质得出∠A=90°,AD=BC=2,由题意得出BE=BC=2,由勾股定理求出AE,即可得出结果.
解答 解:∵四边形ABCD是矩形,BC=2AB,AB=1,
∴AD=BC=2,∠A=90°,
∴BE=BC=2,
∴AE=$\sqrt{B{E}^{2}-A{B}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴DE=AD-AE=2-$\sqrt{3}$.
故答案为:2-$\sqrt{3}$.
点评 本题考查了矩形的性质、勾股定理、同圆的半径相等的性质;熟练掌握矩形的性质,由勾股定理求出AE是解决问题的关键.

练习册系列答案
相关题目
15.下列图形中,是中心对称图形但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
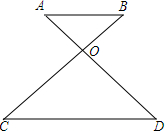 如图,OA:OD=OB:OC=1:2,OB=3.
如图,OA:OD=OB:OC=1:2,OB=3.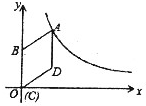 如图,在平面直角坐标系中,菱形ABCD的顶点C与远点O重合,点B在y轴的正半轴上,点A在反比例函数$y=\frac{k}{x}(k>0,x>0)$的图象上,点D的坐标为(4,3),则k的值为( )
如图,在平面直角坐标系中,菱形ABCD的顶点C与远点O重合,点B在y轴的正半轴上,点A在反比例函数$y=\frac{k}{x}(k>0,x>0)$的图象上,点D的坐标为(4,3),则k的值为( )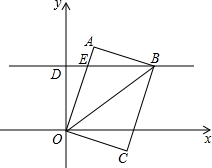 如图,在平面直角坐标系中,有一矩形OABC,OA=8,OC=6,过点D(0,6)作y轴的垂线交OA于点E,点B恰在这条直线上.
如图,在平面直角坐标系中,有一矩形OABC,OA=8,OC=6,过点D(0,6)作y轴的垂线交OA于点E,点B恰在这条直线上.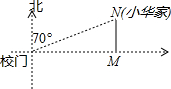 如图,小华家位于校门北偏东70°的方向,和校门的直线距离为4km的N处,则小华家到校门所在街道(东西方向)的距离NM约为1.37km.(用科学计算器计算,结果精确到0.01km).
如图,小华家位于校门北偏东70°的方向,和校门的直线距离为4km的N处,则小华家到校门所在街道(东西方向)的距离NM约为1.37km.(用科学计算器计算,结果精确到0.01km).