计算(1)-22+$\sqrt{(-2{)^2}}$-$\root{3}{-8}$2=8．题目和参考答案——青夏教育精英家教网—

题目内容

2．计算
（1）-2²+$\sqrt{（-2{）^2}}$-$\root{3}{-8}$
（2）2（x-1）²=8．

分析（1）原式第一项利用乘方的意义化简，第二项利用二次根式的性质化简，最后一项利用立方根定义计算即可得到结果；
（2）方程变形后，开方即可求出解．

解答解：（1）原式=-4+2-（-2）
=-4+4
=0；
（2）方程变形得：（x-1）²=4，
开方得：x-1=2或x-1=-2，
解得：x=3或x=-1．

点评此题考查了实数的运算，熟练掌握运算法则是解本题的关键．

练习册系列答案

已知：如图1，△ABC中，AD是角平分线，求证：$\frac{BD}{DC}=\frac{AB}{AC}$
分析：要证$\frac{BD}{DC}=\frac{AB}{AC}$，一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在的三角形相似．现在B、D、C在一直线上，△ABD与△ADC不相似，需要考虑用别的方法换比．
在比例式$\frac{BD}{DC}=\frac{AB}{AC}$中，AC恰是BD、DC、AB的第四比例项，所以考虑过C作CE∥AD，交BA的延长线于E，从而得到BD、DC、AB的第四比例项AE，这样，证明$\frac{BD}{DC}=\frac{AB}{AC}$就可以转化为证AE=AC．
（1）证明：过C作CE∥DA，交BA的延长线于E．（完成以下证明过程）
∴AE=AC（等腰三角形的判定定理）
∴△BAD∽△BEC，∴$\frac{BD}{BC}=\frac{AB}{BE}$（相似三角形的性质）∴$\frac{BD}{DC}=\frac{AB}{AC}$
（2）用三角形内角平分线性质定理解答问题：
已知：如图2，△ABC中，AD是角平分线，AB=5cm，AC=4cm，BC=7cm．
求：BD的长．

13．若把分式$\frac{x+3y}{2x}$的x、y同时缩小12倍，则分式的值（　　）

10．若不等式组$\left\{\begin{array}{l}{x＞2}\\{x＞m}\end{array}\right.$的解集是x＞2，则m的取值范围是（　　）

-2与$\sqrt{{{（-2）}^2}}$

7．

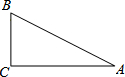如图，在Rt△ABC中，∠C=90°，∠A=30°，BC=1，则AC=$\sqrt{3}$．

14．

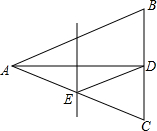如图，△ABC中，AB=AC=13，BC=10，AD平分∠BAC交BC于点D，AD的垂直平分线交AC于点E，连接DE，则△CDE的周长为18．

11．给出下列算式：3²-1²=8=8×1；
5²-3²=16=8×2；
7²-5²=24=8×3；
9²-7²=32=8×4．
（1）观察上面一系列式子，你能发现什么规律？
（2）用含n的式子表示出来（n为正整数）．
（3）计算 2011²-2009²=8032，此时n=1004．

12．计算：
（1）（-2x²）³•x²+（3x⁴）²；　　　　　　
（2）（-$\frac{1}{3}$）^-1+（+8）⁰-2²⁰¹²×（-$\frac{1}{2}$）²⁰¹¹．

试题分类