题目内容
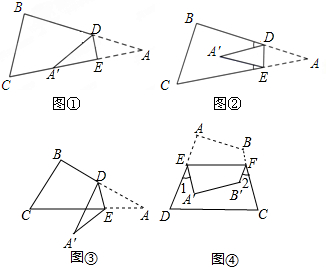
7．
如图，在Rt△ABC中，∠C=90°，∠A=30°，BC=1，则AC=$\sqrt{3}$．
分析 先根据30°角所对的直角边等于斜边的一半得出AB=2BC=2，再利用勾股定理即可求解．
解答 解：∵在Rt△ABC中，∠C=90°，∠A=30°，BC=1，
∴AB=2BC=2，
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$．
故答案为$\sqrt{3}$．
点评 本题考查了含30度角的直角三角形的性质：在直角三角形中，30°角所对的直角边等于斜边的一半．同时考查了勾股定理．
练习册系列答案
尖子生新课堂课时作业系列答案
相关题目
已知点M为某封闭图形边界上一定点，动点P从点M出发，沿其边界顺时针匀速运动一周．设点P运动的时间为x，线段MP的长为y．表示y与x的函数关系的图象大致如图所示，则该封闭图形可能是（ ）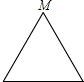
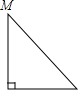
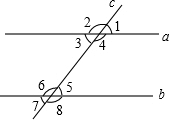如图所示，直线a，b被直线c所截，现给出下列四个条件①∠1=∠5；②∠1=∠7；③∠2+∠3=180°；④∠4=∠7，其中能判定a∥b的条件序号是（ ）
已知，如图，在△ABC中，OB和OC分别平分∠ABC和∠ACB，过O作DE∥BC，分别交AB、AC于点D、E，若DE=8，则线段BD+CE的长为（ ）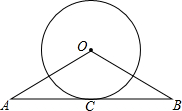
如图，已知直线AB经过⊙O上的点C，且OA=OB，CA=CB．