题目内容
17.下列各组数中互为相反数的是( )| A. | |-2|与2 | B. | -2与$\root{3}{-8}$ | C. | -2与$-\frac{1}{2}$ | D. | -2与$\sqrt{{{(-2)}^2}}$ |
分析 首先根据|-2|=2,可得|-2|与2相等;然后根据$\root{3}{-8}=-2$,可得-2=$\root{3}{-8}$;再根据互为倒数的含义,可得-2与-$\frac{1}{2}$互为倒数;最后根据$\sqrt{{(-2)}^{2}}=2$,可得-2与$\sqrt{{(-2)}^{2}}$互为相反数,据此解答即可.
解答 解:∵|-2|=2,
∴|-2|与2相等;
∵$\root{3}{-8}=-2$,
∴-2=$\root{3}{-8}$;
∵(-2)×(-$\frac{1}{2}$)=1,
∴-2与-$\frac{1}{2}$互为倒数;
∵据$\sqrt{{(-2)}^{2}}=2$,
∴-2与$\sqrt{{(-2)}^{2}}$互为相反数.
故选:D.
点评 (1)此题主要考查了相反数的含义以及求法,要熟练掌握,解答此题的关键是要明确:相反数是成对出现的,不能单独存在;求一个数的相反数的方法就是在这个数的前边添加“-”.
(2)此题还考查了绝对值的非负性,以及互为倒数的含义以及判断,要熟练掌握.
(3)此题还考查了立方根的性质和应用,要熟练掌握,解答此题的关键是要明确:一个数的立方根只有一个,正数的立方根是正数,负数的立方根是负数,0的立方根是0.

练习册系列答案
相关题目
6.若x2+kx+81是一个完全平方式,则k等于( )
| A. | -18 | B. | 9 | C. | 18或-18 | D. | 18 |
7.某批乒乓球的质量检验结果如下:
(1)画出这批乒乓球“优等品”频率的折线统计图;
(2)这批乒乓球“优等品”的概率的估计值是多少?
(3)从这批乒乓球中选择5个黄球、13个黑球、22个红球,它们除颜色外都相同,将它们放入一个不透明的袋中.
①求从袋中摸出一个球是黄球的概率;
②现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后使从袋中摸出一个是黄球的概率不小于$\frac{1}{3}$,问至少取出了多少个黑球?
| 抽取的乒乓球数n | 200 | 500 | 1000 | 1500 | 2000 |
| 优等品频数m | 188 | 471 | 946 | 1426 | 1898 |
| 优等品频率$\frac{m}{n}$ | 0.940 | 0.942 | 0.946 | 0.951 | 0.949 |
(2)这批乒乓球“优等品”的概率的估计值是多少?
(3)从这批乒乓球中选择5个黄球、13个黑球、22个红球,它们除颜色外都相同,将它们放入一个不透明的袋中.
①求从袋中摸出一个球是黄球的概率;
②现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后使从袋中摸出一个是黄球的概率不小于$\frac{1}{3}$,问至少取出了多少个黑球?
 实数a、b在数轴上对应的位置如图,化简$\sqrt{(a+1)^{2}}$+$\sqrt{(b-2)^{2}}$+|a-b|.
实数a、b在数轴上对应的位置如图,化简$\sqrt{(a+1)^{2}}$+$\sqrt{(b-2)^{2}}$+|a-b|.
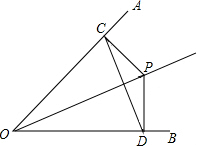 如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.
如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.