题目内容
15.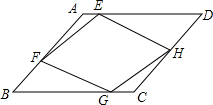 如图,E、F、G、H分别为?ABCD的边AD、AB、BC、CD上的点,且AE=CG,BF=DH.求证:四边形EFGH是平行四边形.
如图,E、F、G、H分别为?ABCD的边AD、AB、BC、CD上的点,且AE=CG,BF=DH.求证:四边形EFGH是平行四边形.
分析 由?ABCD可得∠A=∠C、AB=CD,结合AE=CG得AF=CH,证△AEF≌△CGH得EF=GH,同理可得FG=EH,即可得证.
解答 证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB=CD,
∵BF=DH,
∴AB-BF=CD-DH,即AF=CH,
在△AEF和△CGH中,
∵$\left\{\begin{array}{l}{AF=CH}\\{∠A=∠C}\\{AE=CG}\end{array}\right.$,
∴△AEF≌△CGH(SAS),
∴EF=GH,
同理可得△BGF≌△DEH,
∴FG=EH,
∴四边形EFGH是平行四边形.
点评 本题主要考查平行四边形的判定与性质,根据平行四边形的性质得出AF=CH证得两三角形全等是解题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
6. 如图,AB,CD是⊙O的两条弦,连接AD,BC,若∠BCD=50°,则∠BAD的度数为( )
如图,AB,CD是⊙O的两条弦,连接AD,BC,若∠BCD=50°,则∠BAD的度数为( )
 如图,AB,CD是⊙O的两条弦,连接AD,BC,若∠BCD=50°,则∠BAD的度数为( )
如图,AB,CD是⊙O的两条弦,连接AD,BC,若∠BCD=50°,则∠BAD的度数为( )| A. | 70° | B. | 60° | C. | 50° | D. | 40° |

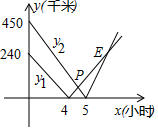 高速公路上依次有3个标志点A、B、C,甲、乙两车分别从A、C两点同时出发,匀速行驶,甲车从A→B→C,乙车从C→B→A,甲、乙两车离B的距离y1、y2(千米)与行驶时间x(小时)之间的函数关系图象如图所示.观察图象,给出下列结论:①A、C之间的路程为690千米;②乙车比甲车每小时快30千米;③4.5小时两车相遇;④点E的坐标为(7,180),其中正确的有①②④(把所有正确结论的序号都填在横线上).
高速公路上依次有3个标志点A、B、C,甲、乙两车分别从A、C两点同时出发,匀速行驶,甲车从A→B→C,乙车从C→B→A,甲、乙两车离B的距离y1、y2(千米)与行驶时间x(小时)之间的函数关系图象如图所示.观察图象,给出下列结论:①A、C之间的路程为690千米;②乙车比甲车每小时快30千米;③4.5小时两车相遇;④点E的坐标为(7,180),其中正确的有①②④(把所有正确结论的序号都填在横线上).