题目内容
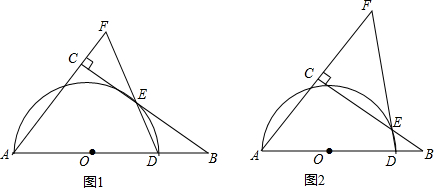
10.若D为等腰直角三角形ABC的BC边上任一点,且DE⊥AD,BE⊥AB.(1)求证:△ADE是等腰直角三角形;
(2)如图,当D在CB上任意运动时,若BC=a,过B作BM⊥BC交AE于M,现给二个结论:①∠BMD的度数不变:②BD+BM+DM值不变,其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论,并求其值.

分析 (1)如图1中,在线段CA取一点F,使得CF=CD.只要证明△ADF≌△DEB.即可推出AD=DE;
(2)②正确.如图2中,作AG⊥BM交BM的延长线于G,在BG 的延长线上截取GH=CD.首先证明四边形ACBG是正方形,再证明△MAH≌△MAD,推出DM=KM,由HM=GM+HG=GM+CD,推出DM=CD+GM.推出BD+BM+DM=BD+BM+CD+MG=BC+BG=2BC=2a即可;
解答 (1)证明:如图1中,在线段CA取一点F,使得CF=CD.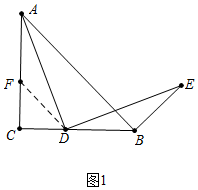
∵∠C=90°,CF=CD,AC=CB,
∴AF=DB,∠CFD=∠CDF=45°,
∴∠AFD=135°,
∵BE⊥AB,∠ABC=45°,
∴∠ABE=90°,
∴∠DBE=135°,
∴∠AFD=∠DBE,
∵AD⊥DE,
∴∠ADE=90°,
∵∠FAD+∠ADC=90°,∠ADC+∠BDE=90°,
∴∠FAD=∠BDE,
在△ADF和△DEB中,
$\left\{\begin{array}{l}{∠FAD=∠BDE}\\{AF=DB}\\{∠AFD=∠DBE}\end{array}\right.$,
∴△ADF≌△DEB.
∴AD=DE,
∵∠ADE=90°,
∴△ADE是等腰直角三角形.
(2)解:②正确.
理由:如图2中,作AG⊥BM交BM的延长线于G,在BG 的延长线上截取GH=CD.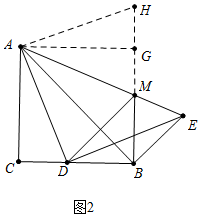
∵∠C=∠CBG=∠AGB=90°,
∴四边形ACBG是矩形,
∵AC=CB,
∴四边形ACBG是正方形,
∴AC=AG,∠ACD=∠AGH=90°,
∴△ACD≌△AGH,
∴AD=AH,∠GAH=∠CAD,
∵∠DAE=45°,
∴∠MAH=∠MAG+∠GAH=∠MAG+∠CAD=45°,
∴∠MAD=∠MAH,∵MA=MA,
∴△MAH≌△MAD,
∴DM=KM,
∵HM=GM+HG=GM+CD,
∴DM=CD+GM.
∴BD+BM+DM=BD+BM+CD+MG=BC+BG=2BC=2a.
∴BD+BM+DM的值是定值.
点评 本题考查等腰直角三角形的性质、全等三角形的判定和性质、正方形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案| A. | y=2x-1 | B. | y=2x+1 | C. | y=-4x+3 | D. | y=2x+7 |
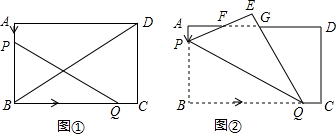
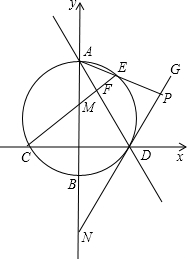 如图,点M在y轴的正半轴上,⊙M交x轴于C、D两点,交y轴于A、B两点,直线y=-2x+6经过A、D两点
如图,点M在y轴的正半轴上,⊙M交x轴于C、D两点,交y轴于A、B两点,直线y=-2x+6经过A、D两点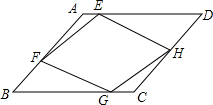 如图,E、F、G、H分别为?ABCD的边AD、AB、BC、CD上的点,且AE=CG,BF=DH.求证:四边形EFGH是平行四边形.
如图,E、F、G、H分别为?ABCD的边AD、AB、BC、CD上的点,且AE=CG,BF=DH.求证:四边形EFGH是平行四边形. 如图,为了测量河的宽度AB,测量人员在高21m的建筑物CD的顶端D处测得河岸B处的俯角为45°,测得河对岸A处的俯角为30°(A,B,C在同一条直线上),则河的宽度AB约为15.3m.
如图,为了测量河的宽度AB,测量人员在高21m的建筑物CD的顶端D处测得河岸B处的俯角为45°,测得河对岸A处的俯角为30°(A,B,C在同一条直线上),则河的宽度AB约为15.3m.