题目内容
20.先化简,再求值:$\frac{x}{{x}^{2}-2x+1}$÷($\frac{x+1}{{x}^{2}-1}$+1),其中x=2$\sqrt{3}$+1.分析 先将分子分母因式分解,然后根据分式的基本性质进行化简求值即可.
解答 解:当x=2$\sqrt{3}$+1
原式=$\frac{x}{({x-1)}^{2}}$÷$\frac{x+1+{x}^{2}-1}{{x}^{2}-1}$
=$\frac{x}{(x-1)^{2}}$×$\frac{(x-1)(x+1)}{x(x+1)}$
=$\frac{1}{x-1}$
=$\frac{1}{2\sqrt{3}}$
=$\frac{\sqrt{3}}{6}$
点评 本题考查分式化简求值,解题的关键是熟练运用因式分解以及分式的基本性质,本题属于基础题型.

练习册系列答案
相关题目
11.不等式组 $\left\{\begin{array}{l}{x+2>0}\\{x-2≤2}\end{array}\right.$ 的解集是( )
| A. | x>-2 | B. | x≤4 | C. | -2<x≤4 | D. | 无解 |
5.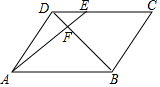 如图,?ABCD中,点E是边DC的一个三等分点,AE交对角线BD于点F,则S△DEF:S△DAF等于( )
如图,?ABCD中,点E是边DC的一个三等分点,AE交对角线BD于点F,则S△DEF:S△DAF等于( )
 如图,?ABCD中,点E是边DC的一个三等分点,AE交对角线BD于点F,则S△DEF:S△DAF等于( )
如图,?ABCD中,点E是边DC的一个三等分点,AE交对角线BD于点F,则S△DEF:S△DAF等于( )| A. | 1:2 | B. | 2:3 | C. | 1:4 | D. | 1:3 |
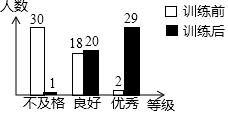 某校九年级700名学生在2016年中考体育考试前对跑步进行了强化训练,在训练前后进行了二次测试,测试成绩都以同一标准(10分为满分)划分成“不及格(7分及以下)”、“良好(9分或8分)”和“优秀(10分)”三个等级.为了了解强化训练的效果,用随机方式抽取了九年级学生中50名学生的前后两次测试成绩的等级,并绘制成如图所示的统计图,试结合图形信息回答下列问题:
某校九年级700名学生在2016年中考体育考试前对跑步进行了强化训练,在训练前后进行了二次测试,测试成绩都以同一标准(10分为满分)划分成“不及格(7分及以下)”、“良好(9分或8分)”和“优秀(10分)”三个等级.为了了解强化训练的效果,用随机方式抽取了九年级学生中50名学生的前后两次测试成绩的等级,并绘制成如图所示的统计图,试结合图形信息回答下列问题: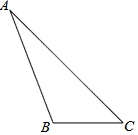 如图,已知△ABC,按要求作图.
如图,已知△ABC,按要求作图.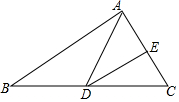 已知D、E分别是△ABC的边BC和边AC的中点,连接DE、AD,若S△ABC=24cm2,则S△DEC=6cm2.
已知D、E分别是△ABC的边BC和边AC的中点,连接DE、AD,若S△ABC=24cm2,则S△DEC=6cm2.