题目内容
15.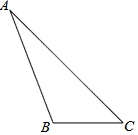 如图,已知△ABC,按要求作图.
如图,已知△ABC,按要求作图.(1)过点A作BC的垂线段AD;
(2)过C作AB、AC的垂线分别交AB于点E、F;
(3)AB=15,BC=7,AC=20,AD=12,求点C到线段AB的距离.
分析 (1)、(2)根据几何语言作图;
(3)利用三角形面积公式得到$\frac{1}{2}$•AB•CE=$\frac{1}{2}$•BC•AD,然后把AB=15,BC=7,AD=12代入计算可求出CE.
解答 解:(1)如图,AD为所作;
(2)如图,CE、CF为所作;
(3)∵S△ABC=$\frac{1}{2}$•AB•CE=$\frac{1}{2}$•BC•AD,
∴CE=$\frac{BC•AD}{AB}$=$\frac{7×12}{15}$=$\frac{28}{5}$,
即点C到线段AB的距离为$\frac{28}{5}$.
点评 本题考查了作图-基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).

练习册系列答案
相关题目
10.不等式组$\left\{\begin{array}{l}{-2x<6}\\{x-2>0}\end{array}\right.$的解集是( )
| A. | x>-3 | B. | x<-3 | C. | x>2 | D. | 无解 |
7.解不等式组:$\left\{\begin{array}{l}{3-2×(x-1)>0}\\{\frac{x+3}{2}-1≤x}\end{array}\right.$,并写出符合不等式组的整数解.
11.今年国庆节期间,武汉市欢乐谷为了吸引广大游客前去游玩,该公司设计一种很刺激的,同时又能给游客带来实惠的游戏.游戏从起点到终点共6关,每一关都有游客上或者下.某一时间段,每一关上下游客的数量统计如下表:(用正数表示上的人数,负数表示下的人数)
(1)到终点还有多少人,表格相应的位置应该填的数是42
(2)若每人每过一关就奖励5元的代金券,问这一时间段公司要准备多少金额的代金券?
| 起点 | A | B | C | D | 终点 | |
| 上的人数 | 28 | 15 | 12 | 7 | 5 | 0 |
| 下的人数 | 0 | -2 | -2 | -10 | -11 |
(2)若每人每过一关就奖励5元的代金券,问这一时间段公司要准备多少金额的代金券?