题目内容
5．
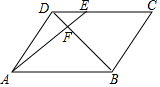如图，?ABCD中，点E是边DC的一个三等分点，AE交对角线BD于点F，则S△DEF：S△DAF等于（ ）| A． | 1：2 | B． | 2：3 | C． | 1：4 | D． | 1：3 |
分析 设DE=a，EC=2a，则CD=3a，由四边形ABCD是平行四边形，推出AB=CD=3a，DE∥AB，推出△DEF∽△BAF，推出$\frac{EF}{AF}$=$\frac{DE}{AB}$=$\frac{a}{3a}$=$\frac{1}{3}$，推出$\frac{{S}_{△DEF}}{{S}_{△ADF}}$=$\frac{EF}{AF}$即可解决问题．
解答 解：设DE=a，EC=2a，则CD=3a，
∵四边形ABCD是平行四边形，
∴AB=CD=3a，DE∥AB，
∴△DEF∽△BAF，
∴$\frac{EF}{AF}$=$\frac{DE}{AB}$=$\frac{a}{3a}$=$\frac{1}{3}$，
∴$\frac{{S}_{△DEF}}{{S}_{△ADF}}$=$\frac{EF}{AF}$=$\frac{1}{3}$，
故选D．
点评 本题考查相似三角形的判定和性质、平行四边形的性质等知识，解题的关键是熟练掌握相似三角形的判定和性质，属于中考常考题型．
练习册系列答案
相关题目
如图，已知AD⊥BD，∠A=55°，∠CDB=35°，求证：AB∥CD．