题目内容
12. 为了增强学生体质,学校鼓励学生多参加体育锻炼,小胖同学马上行动,每天围绕小区进行晨跑锻炼.该小区外围道路近似为如图所示四边形ABCD,已知四边形ABED是正方形,∠DCE=45°,AB=100米.小胖同学某天绕该道路晨跑5圈,时间约为20分钟,求小胖同学该天晨跑的平均速度约为多少米/分?(结果保留整数,$\sqrt{2}$≈1.41)
为了增强学生体质,学校鼓励学生多参加体育锻炼,小胖同学马上行动,每天围绕小区进行晨跑锻炼.该小区外围道路近似为如图所示四边形ABCD,已知四边形ABED是正方形,∠DCE=45°,AB=100米.小胖同学某天绕该道路晨跑5圈,时间约为20分钟,求小胖同学该天晨跑的平均速度约为多少米/分?(结果保留整数,$\sqrt{2}$≈1.41)
分析 首先利用勾股定理求出CD的长度,然后求出小胖每天晨跑的路程,进而求出平均速度.
解答 解:∵ABED是正方形,∠DCE=45°,AB=100米,
∴DE=CE=100米,
在直角三角形DEC中,
DC2=DE2+CE2,即DC=100$\sqrt{2}$,
∴四边形ABCD的周长为100+100+100+100$\sqrt{2}$+100=400+100$\sqrt{2}$,
∵小胖同学某天绕该道路晨跑5圈,时间约为20分钟,
∴小胖每天晨跑的路程为(2000+500$\sqrt{2}$)米,
∴小胖同学该天晨跑的平均速度(2000+500$\sqrt{2}$)÷20=100+25$\sqrt{2}$≈135.25米/分.
点评 本题主要考查了解直角三角形的应用,解题的关键是利用勾股定理求出DC的长度,此题难度不大.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
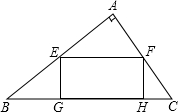 如图,△ABC是一块直角三角形材料,∠BAC=90°,BC=100cm,AB=80cm,要把它加工成矩形零件,使矩形一边在BC上,其余两个顶点分别在AB、AC上.
如图,△ABC是一块直角三角形材料,∠BAC=90°,BC=100cm,AB=80cm,要把它加工成矩形零件,使矩形一边在BC上,其余两个顶点分别在AB、AC上.