题目内容
2.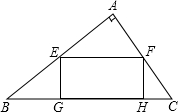 如图,△ABC是一块直角三角形材料,∠BAC=90°,BC=100cm,AB=80cm,要把它加工成矩形零件,使矩形一边在BC上,其余两个顶点分别在AB、AC上.
如图,△ABC是一块直角三角形材料,∠BAC=90°,BC=100cm,AB=80cm,要把它加工成矩形零件,使矩形一边在BC上,其余两个顶点分别在AB、AC上.(1)请求出sinB的值;
(2)当顶点E位于AB上何处时,这个矩形零件的面积最大?并求出最大值.
分析 (1)利用勾股定理求得AC的长度,然后利用锐角三函数的定义求出sinB的值;
(2)根据题意得出△AEF∽△ABC,进而表示出AE的长,再利用二次函数最值求法得出答案.
解答  解:(1)∵在△ABC中,∠BAC=90°,BC=100cm,AB=80cm,
解:(1)∵在△ABC中,∠BAC=90°,BC=100cm,AB=80cm,
∴AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=$\sqrt{10{0}^{2}-8{0}^{2}}$=60(cm),
∴sinB=$\frac{AC}{BC}$=$\frac{60}{100}$=$\frac{3}{5}$,即sinB的值是$\frac{3}{5}$;
(2)如图,过点A作BC边上的高线AM,交EF于点N.
由$\frac{1}{2}$AB•AC=$\frac{1}{2}$BC•AM得到:AM=$\frac{80×60}{100}$=48(cm)
∵由题意知,EF∥BC,
∴△AEF∽△ABC,
∴$\frac{AN}{AM}$=$\frac{EF}{BC}$,即$\frac{AN}{48}$=$\frac{EF}{100}$,
∴EF=$\frac{25}{12}$AN,
∴S矩形EFHG=EF•NM=$\frac{25}{12}$AN•(48-AN)=-100AN-$\frac{25}{12}$AN2=-$\frac{25}{12}$(AN-24)2+1200.
当AN=24时,这个矩形零件的面积最大,最大值是1200cm2.
由$\frac{AN}{AE}$=$\frac{3}{5}$得到:AE=$\frac{5}{3}$AN=40(cm).
∴当点E是AB的中点时,这个矩形零件的面积最大,最大值是1200cm2.
点评 本题考查了解直角三角形的应用、相似三角形的应用以及二次函数的最值问题,根据题意表示出AE的长是解题关键.

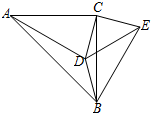 如图,在△ABC中,∠ACB=90°,∠CAD=30°,AC=BC=AD,CE⊥CD,且CE=CD,连接BD、DE、BE,则下列结论:①∠ECA=165°,②BE=BC;③AD=BE;④CD=BD.其中正确的是( )
如图,在△ABC中,∠ACB=90°,∠CAD=30°,AC=BC=AD,CE⊥CD,且CE=CD,连接BD、DE、BE,则下列结论:①∠ECA=165°,②BE=BC;③AD=BE;④CD=BD.其中正确的是( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
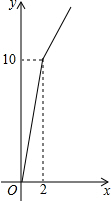 某玉米种子的价格为a元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折.某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出函数图象.如表是该科技人员绘制的图象和表格的不完整资料,已知点A的坐标为(2,10).请你结合表格和图象:
某玉米种子的价格为a元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折.某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出函数图象.如表是该科技人员绘制的图象和表格的不完整资料,已知点A的坐标为(2,10).请你结合表格和图象:| 付款金额(元) | a | 7.5 | 10 | 12 | b |
| 购买量(千克) | 1 | 1.5 | 2 | 2.5 | 3 |
(2)求出当x>2时,y关于x的函数解析式;
(3)甲农户将8.8元钱全部用于购买玉米种子,乙农户购买了4500克该玉米种子,分别计算他们的购买量和付款金额.
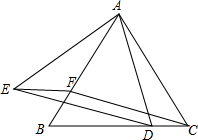 如图,△ABC为等边三角形,D、F分别为BC、AB上的点,且CD=BF.
如图,△ABC为等边三角形,D、F分别为BC、AB上的点,且CD=BF. 为了增强学生体质,学校鼓励学生多参加体育锻炼,小胖同学马上行动,每天围绕小区进行晨跑锻炼.该小区外围道路近似为如图所示四边形ABCD,已知四边形ABED是正方形,∠DCE=45°,AB=100米.小胖同学某天绕该道路晨跑5圈,时间约为20分钟,求小胖同学该天晨跑的平均速度约为多少米/分?(结果保留整数,$\sqrt{2}$≈1.41)
为了增强学生体质,学校鼓励学生多参加体育锻炼,小胖同学马上行动,每天围绕小区进行晨跑锻炼.该小区外围道路近似为如图所示四边形ABCD,已知四边形ABED是正方形,∠DCE=45°,AB=100米.小胖同学某天绕该道路晨跑5圈,时间约为20分钟,求小胖同学该天晨跑的平均速度约为多少米/分?(结果保留整数,$\sqrt{2}$≈1.41)