题目内容
20．已知关于x的一元二次方程x2-kx-2=0，（1）求证无论k为何值，方程总有两个不相等的实数根？
（2）给k取一个你喜欢的值，并求解这个方程．
分析 （1）根据方程各项的系数结合根的判别式即可得出△=k2+8≥8，由此可得出无论k为何值，方程总有两个不相等的实数根；
（2）将k=1代入原方程中，再用分解因式法解方程即可得出结论．
解答 （1）证明：在方程x2-kx-2=0中，
△=（-k）2-4×1×（-2）=k2+8≥8，
∴无论k为何值，方程总有两个不相等的实数根；
（2）解：当k=1时，方程为x2-x-2=（x+1）（x-2）=0，
解得：x1=-1，x2=2．
点评 本题考查了根的判别式以及解一元二次方程，根据根的判别式△=k2+8的符号确定方程解的情况是解题的关键．
练习册系列答案
相关题目
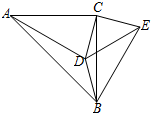如图，在△ABC中，∠ACB=90°，∠CAD=30°，AC=BC=AD，CE⊥CD，且CE=CD，连接BD、DE、BE，则下列结论：①∠ECA=165°，②BE=BC；③AD=BE；④CD=BD．其中正确的是（ ）
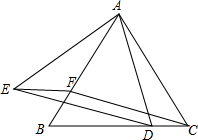如图，△ABC为等边三角形，D、F分别为BC、AB上的点，且CD=BF．
已知：如图，点E是线段AB的中点，∠A=∠B，∠AED=∠BEC．求证：CE=DE．
为了增强学生体质，学校鼓励学生多参加体育锻炼，小胖同学马上行动，每天围绕小区进行晨跑锻炼．该小区外围道路近似为如图所示四边形ABCD，已知四边形ABED是正方形，∠DCE=45°，AB=100米．小胖同学某天绕该道路晨跑5圈，时间约为20分钟，求小胖同学该天晨跑的平均速度约为多少米/分？（结果保留整数，$\sqrt{2}$≈1.41）