题目内容
2．在阳光下，身高1.7m的小强在地面上的影长为2m，在同一时刻，测得学校的旗杆在地面上的影长为18m．则旗杆的高度为15.3m．分析 利用在同一时刻身高与影长成比例计算．
解答 解：根据题意可得：设旗杆高为x．
根据在同一时刻身高与影长成比例可得：$\frac{1.7}{2}$=$\frac{x}{18}$，
解得：x=15.3．
故答案为：15.3．
点评 本题考查了相似三角形的应用，只要是把实际问题抽象到相似三角形中，利用相似三角形的相似比，列出方程，通过解方程求出旗杆的高度，体现了方程的思想．
练习册系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
13．
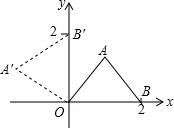将等腰直角三角形AOB按图放置，然后绕O点逆时针旋转90°至A′OB′位置，点B（2，0），则A的坐标（ ）
将等腰直角三角形AOB按图放置，然后绕O点逆时针旋转90°至A′OB′位置，点B（2，0），则A的坐标（ ）| A． | （1，1） | B． | （$\sqrt{2}$，$\sqrt{2}$） | C． | （-1，1） | D． | （$-\sqrt{2}$，$\sqrt{2}$） |
17．下列说法错误的说法有几个（ ）
①全等三角的对应边相等；
②全等三角形的对应角相等；
③全等三角形的面积相等；
④全等三角形的周长相等；
⑤有两边和第三边上的高对应相等的两个三角形全等；
⑥全等三角形的对应边上的中线相等．
①全等三角的对应边相等；
②全等三角形的对应角相等；
③全等三角形的面积相等；
④全等三角形的周长相等；
⑤有两边和第三边上的高对应相等的两个三角形全等；
⑥全等三角形的对应边上的中线相等．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 5个 |
7．
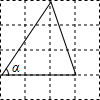如图，在4×4的正方形网格中，tanα的值等于（ ）
如图，在4×4的正方形网格中，tanα的值等于（ ）| A． | $\frac{{2\sqrt{13}}}{13}$ | B． | $\frac{{3\sqrt{13}}}{13}$ | C． | $\frac{3}{2}$ | D． | $\frac{2}{3}$ |
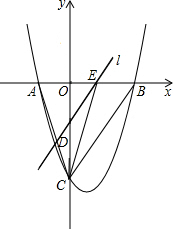如图，抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-9与x轴交于A、B两点，与y轴交于点C，连接BC、AC．
12．下列运算正确的是（ ）
| A． | （x3）2=x5 | B． | x2+x3=x5 | C． | 3-2=$\frac{1}{9}$ | D． | 6x3÷（-3x2）=2x |