题目内容
10.已知关于x的方程x2+x+m=0有两个不相等的实数根,则m的取值范围是m<$\frac{1}{4}$.分析 关于x的方程x2+x+m=0有两个不相等的实数根,即判别式△=b2-4ac>0,即可得到关于m的不等式,从而求得m的范围.
解答 解:∵a=1,b=1,c=m,
∴△=b2-4ac=(1)2-4×1×m=1-4m>0,
解得:m<$\frac{1}{4}$.
故答案为m<$\frac{1}{4}$.
点评 本题考查了一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.下列各组数中,能构成三角形的是( )
| A. | 1,2,4 | B. | 4,5,9 | C. | 4,6,8 | D. | 12,5,5 |
15.若函数y=$\frac{x-2}{{x}^{2}-1}$的函数值为0,则自变量x的值为( )
| A. | 2 | B. | -1 | C. | ±1 | D. | 1 |
19.在学习“用直尺和圆规作一个角等于已知角”时,教科书介绍如下:
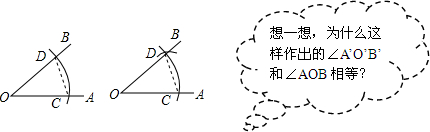
作法:
(1)如图所示,以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
(2)画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;
(3)以点C′为圆心,CD长为半径画弧,与第2步中所画的弧相交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB
对于“想一想”中的问题,下列回答正确的是( )

作法:
(1)如图所示,以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
(2)画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;
(3)以点C′为圆心,CD长为半径画弧,与第2步中所画的弧相交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB
对于“想一想”中的问题,下列回答正确的是( )
| A. | 根据“边边边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB | |
| B. | 根据“边角边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB | |
| C. | 根据“角边角”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB | |
| D. | 根据“角角边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB |
 如图是一数值转换机,若输入的x为-4,则输出的结果为10.
如图是一数值转换机,若输入的x为-4,则输出的结果为10. 如图,在△ABC中,AB=AC,点D在AC边的右侧,连接DA、DB、DC,若AD=DC,∠ADB=∠ACB,AD=5,BD=11,则BC边的长为$\frac{24}{5}$$\sqrt{5}$.
如图,在△ABC中,AB=AC,点D在AC边的右侧,连接DA、DB、DC,若AD=DC,∠ADB=∠ACB,AD=5,BD=11,则BC边的长为$\frac{24}{5}$$\sqrt{5}$.