题目内容
7．
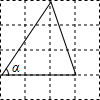如图，在4×4的正方形网格中，tanα的值等于（ ）| A． | $\frac{{2\sqrt{13}}}{13}$ | B． | $\frac{{3\sqrt{13}}}{13}$ | C． | $\frac{3}{2}$ | D． | $\frac{2}{3}$ |
分析 直接根据锐角三角函数的定义即可得出结论．
解答 
解：∵AD⊥BC，AD=3，BD=2，
∴tanα=$\frac{AD}{BD}$=$\frac{3}{2}$．
故选C．
点评 本题考查的是锐角三角函数的定义，熟记锐角三角函数的定义是解答此题的关键．
练习册系列答案
相关题目
如图所示，是由5个大小相同的立方体搭起来的一个几何体，则从左面看到的它的形状图是（ ）
如图是一数值转换机，若输入的x为-4，则输出的结果为10．
15．若函数y=$\frac{x-2}{{x}^{2}-1}$的函数值为0，则自变量x的值为（ ）
| A． | 2 | B． | -1 | C． | ±1 | D． | 1 |
19．在学习“用直尺和圆规作一个角等于已知角”时，教科书介绍如下：
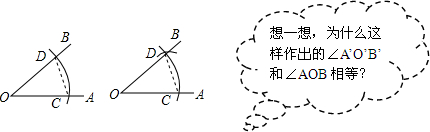
作法：
（1）如图所示，以点O为圆心，任意长为半径画弧，分别交OA，OB于点C，D；
（2）画一条射线O′A′，以点O′为圆心，OC长为半径画弧，交O′A′于点C′；
（3）以点C′为圆心，CD长为半径画弧，与第2步中所画的弧相交于点D′；
（4）过点D′画射线O′B′，则∠A′O′B′=∠AOB
对于“想一想”中的问题，下列回答正确的是（ ）
作法：
（1）如图所示，以点O为圆心，任意长为半径画弧，分别交OA，OB于点C，D；
（2）画一条射线O′A′，以点O′为圆心，OC长为半径画弧，交O′A′于点C′；
（3）以点C′为圆心，CD长为半径画弧，与第2步中所画的弧相交于点D′；
（4）过点D′画射线O′B′，则∠A′O′B′=∠AOB
对于“想一想”中的问题，下列回答正确的是（ ）
| A． | 根据“边边边”可知，△C′O′D′≌△COD，所以∠A′O′B′=∠AOB | |
| B． | 根据“边角边”可知，△C′O′D′≌△COD，所以∠A′O′B′=∠AOB | |
| C． | 根据“角边角”可知，△C′O′D′≌△COD，所以∠A′O′B′=∠AOB | |
| D． | 根据“角角边”可知，△C′O′D′≌△COD，所以∠A′O′B′=∠AOB |