题目内容
13.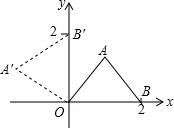 将等腰直角三角形AOB按图放置,然后绕O点逆时针旋转90°至A′OB′位置,点B(2,0),则A的坐标( )
将等腰直角三角形AOB按图放置,然后绕O点逆时针旋转90°至A′OB′位置,点B(2,0),则A的坐标( )| A. | (1,1) | B. | ($\sqrt{2}$,$\sqrt{2}$) | C. | (-1,1) | D. | ($-\sqrt{2}$,$\sqrt{2}$) |
分析 利用勾股定理求出OA的长度,根据旋转变换只改变图形的位置不改变图形的形状与大小求出OA′的长,过点A′作A′C⊥x轴于点C,求出∠A′OC的度数为45°,然后解直角三角形求出OC、A′C,写出点A′的坐标即可.
解答  解:∵△OAB是等腰直角三角形,点B(2,0),
解:∵△OAB是等腰直角三角形,点B(2,0),
∴2OA2=OB2=4,
∴OA=$\sqrt{2}$,
∵OA′是OA旋转得到,
∴OA′=OA=$\sqrt{2}$,
过点A′作A′C⊥x轴于点C,
∵∠AOB=45°,旋转角为90°,
∴∠A′OC=180°-45°-90°=45°,
∴A′C=OC=$\frac{\sqrt{2}}{2}$OA′=1,
所以,点A′(-1,1).
故选C.
点评 本题考查了坐标与图形的性质-旋转,根据旋转变换的性质求出OA′的长度,作辅助线构造出直角三角形是解题的关键,作出图形更形象直观.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
4. 正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2015次后,数轴上数2015所对应的点是( )
正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2015次后,数轴上数2015所对应的点是( )
 正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2015次后,数轴上数2015所对应的点是( )
正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2015次后,数轴上数2015所对应的点是( )| A. | 点C | B. | 点D | C. | 点A | D. | 点B |
5.下列各组数中,能构成三角形的是( )
| A. | 1,2,4 | B. | 4,5,9 | C. | 4,6,8 | D. | 12,5,5 |
3.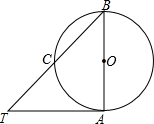 如图,AB是⊙O的直径,AT为⊙O的切线,∠ABT=45°,则下列结论中正确的有( )①∠T=45°;②AT=BA;③∠TAB=90°;④点C为BT中点.
如图,AB是⊙O的直径,AT为⊙O的切线,∠ABT=45°,则下列结论中正确的有( )①∠T=45°;②AT=BA;③∠TAB=90°;④点C为BT中点.
 如图,AB是⊙O的直径,AT为⊙O的切线,∠ABT=45°,则下列结论中正确的有( )①∠T=45°;②AT=BA;③∠TAB=90°;④点C为BT中点.
如图,AB是⊙O的直径,AT为⊙O的切线,∠ABT=45°,则下列结论中正确的有( )①∠T=45°;②AT=BA;③∠TAB=90°;④点C为BT中点.| A. | ①② | B. | ①②③ | C. | ①②③④ | D. | ①②④ |
 如图是一数值转换机,若输入的x为-4,则输出的结果为10.
如图是一数值转换机,若输入的x为-4,则输出的结果为10.