题目内容
11.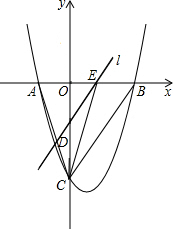 如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合).过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值并此时写出点E坐标.
分析 (1)根据抛物线解析式,可求出A、B、C的坐标,继而可得出AB和OC的长;
(2)根据ED∥BC,可判断△AED∽△ABC,再由相似三角形的面积比等于相似比平方,可得出s关于m的函数关系式,结合题意可得m的取值范围;
(3)根据S△EDC=S△AEC-S△AED,可得△CDE的面积关于m的表达式,利用配方法可求出△CDE面积的最大值,进而得出EO的长,即可得出E点坐标.
解答 解:(1)在y=$\frac{1}{2}$x2-$\frac{3}{2}$x-9中,
令x=0,得y=-9,
∴C(0,-9);
令y=0,即0=$\frac{1}{2}$x2-$\frac{3}{2}$x-9,
解得:x1=-3,x2=6,
∴A(-3,0)、B(6,0),
∴AB=9,OC=9.
(2)∵ED∥BC,
∴△AED∽△ABC,
∴$\frac{{S}_{△AED}}{{S}_{△ABC}}$=($\frac{AE}{AB}$)2,即:$\frac{s}{\frac{1}{2}×9×9}$=($\frac{m}{9}$)2,
∴s=$\frac{1}{2}$m2(0<m<9).
(3)∵S△AEC=$\frac{1}{2}$AE•OC=$\frac{9}{2}$m,S△AED=s=$\frac{1}{2}$m2,
∴S△EDC=S△AEC-S△AED=-$\frac{1}{2}$m2+$\frac{9}{2}$m=-$\frac{1}{2}$(m-$\frac{9}{2}$)2+$\frac{81}{8}$,
当m=$\frac{9}{2}$时,S△EDC取得最大,最大值为$\frac{81}{8}$.
故△CDE的最大面积为$\frac{81}{8}$,
此时,OE=AE-AO=$\frac{9}{2}$-3=$\frac{3}{2}$,
故E点坐标为:($\frac{3}{2}$,0).
点评 本题考查了二次函数的综合,涉及了相似三角形的判定与性质、配方法求二次函数最值等知识,正确利用相似三角形的判定与性质得出s与m的函数关系是解题关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案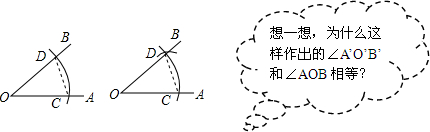
作法:
(1)如图所示,以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
(2)画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;
(3)以点C′为圆心,CD长为半径画弧,与第2步中所画的弧相交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB
对于“想一想”中的问题,下列回答正确的是( )
| A. | 根据“边边边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB | |
| B. | 根据“边角边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB | |
| C. | 根据“角边角”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB | |
| D. | 根据“角角边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB |
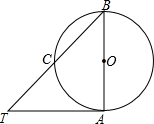 如图,AB是⊙O的直径,AT为⊙O的切线,∠ABT=45°,则下列结论中正确的有( )①∠T=45°;②AT=BA;③∠TAB=90°;④点C为BT中点.
如图,AB是⊙O的直径,AT为⊙O的切线,∠ABT=45°,则下列结论中正确的有( )①∠T=45°;②AT=BA;③∠TAB=90°;④点C为BT中点.| A. | ①② | B. | ①②③ | C. | ①②③④ | D. | ①②④ |
 如图,在△ABC中,AB=AC,点D在AC边的右侧,连接DA、DB、DC,若AD=DC,∠ADB=∠ACB,AD=5,BD=11,则BC边的长为$\frac{24}{5}$$\sqrt{5}$.
如图,在△ABC中,AB=AC,点D在AC边的右侧,连接DA、DB、DC,若AD=DC,∠ADB=∠ACB,AD=5,BD=11,则BC边的长为$\frac{24}{5}$$\sqrt{5}$. 如图,在△ABC中,∠A=90°,AB=AC,O是BC的中点,如果在AB和AC上分别有一个动点M、N在移动,且在移动时保持AN=BM.
如图,在△ABC中,∠A=90°,AB=AC,O是BC的中点,如果在AB和AC上分别有一个动点M、N在移动,且在移动时保持AN=BM.