题目内容
14.“a,b两数差的平方除以它们平方的和”列代数式是$\frac{(a-b)^{2}}{{a}^{2}+{b}^{2}}$.分析 首先求得a,b两数差的平方为(a-b)2,它们平方的和为(a2+b2),由此进一步求得答案即可.
解答 解:“a,b两数差的平方除以它们平方的和”列代数式是$\frac{(a-b)^{2}}{{a}^{2}+{b}^{2}}$.
故答案为:$\frac{(a-b)^{2}}{{a}^{2}+{b}^{2}}$.
点评 此题考查列代数式,理解题意,掌握基本的计算方法是解决问题的关键.

练习册系列答案
相关题目
4. 正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2015次后,数轴上数2015所对应的点是( )
正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2015次后,数轴上数2015所对应的点是( )
 正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2015次后,数轴上数2015所对应的点是( )
正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2015次后,数轴上数2015所对应的点是( )| A. | 点C | B. | 点D | C. | 点A | D. | 点B |
5.下列各组数中,能构成三角形的是( )
| A. | 1,2,4 | B. | 4,5,9 | C. | 4,6,8 | D. | 12,5,5 |
9.抛物线y=(x+1)(x-3)的对称轴是直线( )
| A. | x=-1 | B. | x=1 | C. | x=-3 | D. | x=3 |
19.在学习“用直尺和圆规作一个角等于已知角”时,教科书介绍如下:
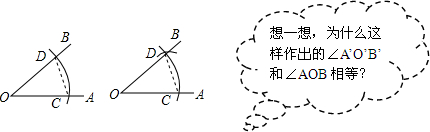
作法:
(1)如图所示,以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
(2)画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;
(3)以点C′为圆心,CD长为半径画弧,与第2步中所画的弧相交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB
对于“想一想”中的问题,下列回答正确的是( )

作法:
(1)如图所示,以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
(2)画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;
(3)以点C′为圆心,CD长为半径画弧,与第2步中所画的弧相交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB
对于“想一想”中的问题,下列回答正确的是( )
| A. | 根据“边边边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB | |
| B. | 根据“边角边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB | |
| C. | 根据“角边角”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB | |
| D. | 根据“角角边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB |
3.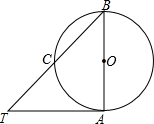 如图,AB是⊙O的直径,AT为⊙O的切线,∠ABT=45°,则下列结论中正确的有( )①∠T=45°;②AT=BA;③∠TAB=90°;④点C为BT中点.
如图,AB是⊙O的直径,AT为⊙O的切线,∠ABT=45°,则下列结论中正确的有( )①∠T=45°;②AT=BA;③∠TAB=90°;④点C为BT中点.
 如图,AB是⊙O的直径,AT为⊙O的切线,∠ABT=45°,则下列结论中正确的有( )①∠T=45°;②AT=BA;③∠TAB=90°;④点C为BT中点.
如图,AB是⊙O的直径,AT为⊙O的切线,∠ABT=45°,则下列结论中正确的有( )①∠T=45°;②AT=BA;③∠TAB=90°;④点C为BT中点.| A. | ①② | B. | ①②③ | C. | ①②③④ | D. | ①②④ |
4.下列变形是属于移项的是( )
| A. | 由2x=2,得x=1 | B. | 由$\frac{x}{2}$=-1,得x=-2 | ||
| C. | 由3x-$\frac{7}{2}$=0,得3x=$\frac{7}{2}$ | D. | 由-2x-2=0,得x=-1 |