题目内容
3. 如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,连接CE,作BF⊥CE,垂足为F,则tan∠FBC的值为$\frac{1}{3}$.
如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,连接CE,作BF⊥CE,垂足为F,则tan∠FBC的值为$\frac{1}{3}$.
分析 首先根据以B为圆心BC为半径画弧交AD于点E,判断出BE=BC=5;然后根据勾股定理,求出AE的值是多少,进而求出DE的值是多少;再根据勾股定理,求出CE的值是多少,再根据BC=BE,BF⊥CE,判断出点F是CE的中点,据此求出CF、BF的值各是多少;最后根据角的正切的求法,求出tan∠FBC的值是多少即可.
解答 解:∵以B为圆心BC为半径画弧交AD于点E,
∴BE=BC=5,
∴AE=$\sqrt{B{E}^{2}-A{B}^{2}}$,
∴DE=AD-AE=5-4=1,
∴CE=$\sqrt{C{D}^{2}+D{E}^{2}}$,
∵BC=BE,BF⊥CE,
∴点F是CE的中点,
∴CF=$\frac{1}{2}$,
∴BF=$\sqrt{B{C}^{2}-C{F}^{2}}$=$\frac{3\sqrt{10}}{2}$,
∴tan∠FBC=$\frac{CF}{BF}$,
即tan∠FBC的值为$\frac{1}{3}$.
故答案是:$\frac{1}{3}$.
点评 此题还考查了锐角三角函数的定义,要熟练掌握,解答此题的关键是要明确一个角的正弦、余弦、正切的求法.

练习册系列答案
相关题目
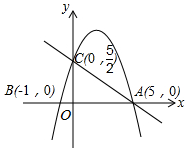 如图,在平面直角坐标系中,已知抛物线y=ax2+bx+c与x轴交于A(5,0),B(-1,0)两点,与y轴交于点C(0,$\frac{5}{2}$).
如图,在平面直角坐标系中,已知抛物线y=ax2+bx+c与x轴交于A(5,0),B(-1,0)两点,与y轴交于点C(0,$\frac{5}{2}$).